Language Log

Rats beat Yalies: Doing better by getting less information?

Louis Menand's review of Philip Tetlock’s book “Expert Political Judgment" makes the point that in "more than a hundred studies that have pitted experts against statistical or actuarial formulas, ... the people either do no better than the formulas or do worse". Menand suggests that the experts' downfall "is exactly the trouble that all human beings have: we fall in love with our hunches, and we really, really hate to be wrong". Tetlock puts it like this (p. 40): "the refusal to accept the inevitability of error -- to acknowledge that some phenomena are irreducibly probabilistic -- can be harmful. Political observers ... look for patterns in random concatenations of events. They would do better by thinking less."

Tetlock illustrates this point with an anecdote about an experiment that "pitted the predictive abilities of a classroom of Yale undergraduates against those of a single Norwegian rat". The experiment involves predicting the availability of food in one arm of a T-shaped maze.The rat wins, by learning quickly that is should always head for the arm in which food is more commonly available -- betting on the maximum-likelihood outcome -- while the undergrads place their bets in more complicated ways, perhaps trying to find patterns in the sequence of trials. They guess correctly on individual trials less often than the rat does, although their overall allocation of guesses matches the relative probability of finding food the two arms very accurately.

This is a good story, and Tetlock's description of the facts is true, as far as it goes. But one crucial thing is omitted, and as a result, Tetlock's interpretation of the facts, repeated with some psychological embroidery by Menand, is entirely wrong. As usual, the true explanation is simpler as well as more interesting than the false one. It illustrates a beautifully simple mathematical model of learning and behavior, which accounts for a wide range of experimental and real-world data besides this classroom demonstration. And there's even a connection, I believe, to the cultural evolution of language.

The same experiments are described in a similar way (though with slightly different numbers) on pp. 351-352 of Randy Gallistel's wonderful book "The Organization of Learning" (which MIT Press has unconscionably allowed to remain out of print for many years). These experiments are examples of a paradigm called "probability learning" or "expected rate learning", in which the subject (human, rat or other) is asked to choose on each trial among two or more alternatives, where the reward and/or feedback is varied among the alternatives probabilistically.

Tetlock suggests that humans perform worse in this experiment because we have a higher-order, more abstract intelligence than rats do: "Human performance suffers [relative to the rat] because we are, deep down, deterministic thinkers with an aversion to probabilistic strategies... We insist on looking for order in random sequences." Menand, on the other hand, thinks it's just vanity:

The students looked for patterns of left-right placement, and ended up scoring only fifty-two per cent, an F. The rat, having no reputation to begin with, was not embarrassed about being wrong two out of every five tries. But Yale students, who do have reputations, searched for a hidden order in the sequence. They couldn’t deal with forty-per-cent error, so they ended up with almost fifty-per-cent error.

Tetlock may be right that we humans like deterministic explanations, at least as a rational reconstruction of our ideas. And Menand may be right about the anxieties of Yale students. However, both are entirely wrong about this experiment. It's not about the difference between humans and animals, or between Yalies and rats. It's about information. The students were given different information than the rat was, and each subject, human or animal, reacted according to its experience.

As Randy Gallistel, who helped run the experiments, explains:

They [the undergraduates] were greatly surprised to be shown when the demonstration was over that the rat's behavior was more intelligent than their own. We did not lessen their discomfiture by telling them that if the rat chose under the same conditions they did -- under a correction procedure whereby on every trial it ended up knowing which side was the rewarded side -- it too would match the relative frequencies of its initial side choices to the relative frequencies of the payoffs (Graff, Bullock, and Bitterman 1964; Sutherland and Mackintosh 1971, p. 406f).

And if the students had chosen under the same conditions as the rat, they too would have been "maximizers", zeroing in on the more-likely alternative and choosing it essentially all the time.

To see the trick, we have to start by describing the apparatus a little more carefully. On a randomly-selected 75% of the trials, the left-hand side of the T was "armed" with a food pellet; on the other 25% of the trials, the right-hand side was. (These are Gallistel's numbers -- Tetlock specifies 60%/40%.) On trials when the rat took the "armed" side of the maze, it was rewarded with a food pellet. Otherwise, it got nothing. But what about the students? Well, on top of each arm of the maze was a shielded light bulb, visible to the students but not to the rat. When the rat pressed the feeder bar, the light bulb over the armed feeder went on -- whether this was the side the rat chose, or not.

Why does this matter? Why does the extra feedback lead the students to choose a strategy that (in this case) makes worse predictions?

For an authoritative review of this overall area of research, find yourself a used copy of Gallistel's book. But here's a slightly oversimplified account of what's going on in this particular case.

We start with a version of the "linear operator model" of Bush & Mosteller 1951:

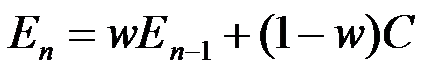
This equation tells us how to update the time-step n estimate E_n (of resource density, or event probability, etc.) as a function of the estimate at time n-1 and the current experience C. The update could hardly be simpler: it's just a linear combination (i.e. a weighted sum) of the previous estimate and the current experience. In this simplest version of the model, there's just one parameter, the memory constant w, which tells us how much to discount previous belief in favor of current experience.

Electrical engineers will recognize this as a "leaky integrator", a first-order recursive filter. Its impulse response is obviously just a decaying exponential. It can easily be implemented in biochemical as well as neural circuitry, so that I would expect to find analogs of this sort of learning even in bacteria.

To apply this model to the rat, we'll maintain two E's -- one estimating the probability that there will be a food pellet in the left-hand maze arm, and the other estimating the same thing for the right-hand arm. (The rat doesn't know that the alternatives are made exclusive by the experimenters.) And we'll assume the golden rule of expected rate learning, expressed by Gallistel as follows:

[W]hen confronted with a choice between alternatives that have different expected rates for the occurrence of some to-be-anticipated outcome, animals, human and otherwise, proportion their choices in accord with the relative expected rates…

On trials where the rat chooses correctly and gets a food pellet, the model's "current experience" C is 1 for the maze arm where the pellet was found, and 0 for the other arm. On trials where the rat chooses wrong and gets no reward, the "current experience" is 0 for both arms.

If we set the model's time-constant w=0.3, and put the food pellet on the left 75% of the time and on the right 25% of the time, and start the rat out with estimates of 0.5 on both sides, and have the rat choose randomly on each trial based on the ratio of its estimates for the "patch profitability" of the two sides, then the model's estimates will look like this:

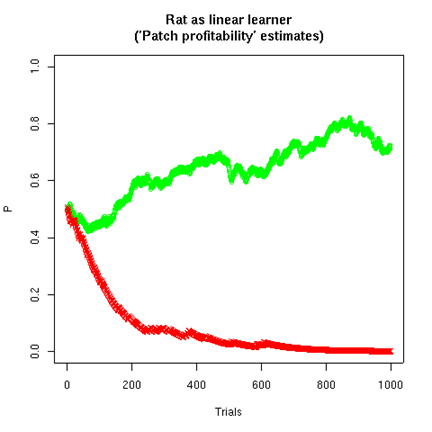
Note that the estimates for the two sides are not complementary. The estimate for the higher-rate side tends towards the true rate (here 75%). The estimate for the lower-rate side tends towards zero, because the (modeled) rat increasingly tends to choose the higher-rate side. If we plot the probabilities of choosing the two sides, based on the "patch profitability ratio" model, we can see that the model is learning to "maximize", i.e. to choose the higher-probability side.

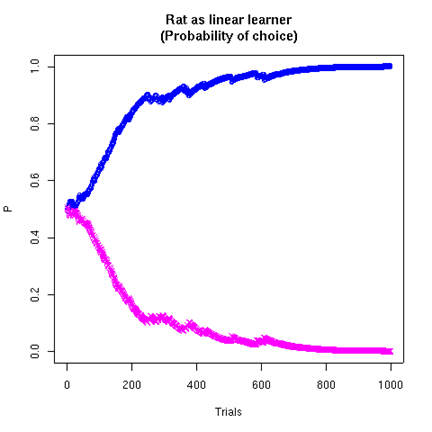
At the asymptotic point of choosing the left side all the time, the rat will be rewarded 75% of the time. (I suspect that rats actually learn faster than this model does, i.e. they act as if they have a lower value for w.)

To model the undergraduates, we use exactly the same model. However, the information coming in is different. On each trial, one of the two lights goes on, and therefore that side's estimate is updated based on a "current experience" of 1, while the other side's estimate is update based on a "current experience" of 0. Everything else is the same -- but the model's behavior is different:

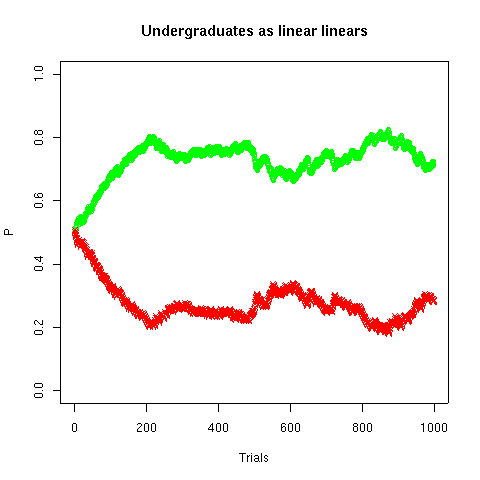
The estimates for the two sides are complementary, and tend towards 0.75 and 0.25. Therefore the students' probability of choice also tends towards 0.75 for the left-hand side, and 0.25 for the right-hand side. Their overall probability of being correct will tend toward 0.75*0.75 + 0.25*0.25 = 0.625, i.e. 62.5%, which is lower than the rat's 75%.

So as it turns out, the rat and the students were arguably applying the same behavioral rule to the same sort of estimate of the situation, and using the same simple learning algorithm to derive that estimate. The difference was not their interest in deterministic theories, nor their concern for their reputations. The difference was simply that the students got more information than the rat did.

At least, there's a simple model that predicts the difference in those terms; and the predictions of that model are apparently confirmed by the results of many thousands of other published experiments in probability learning and expected rate learning.

But why does more information make for worse performance? We're used to seeing evolution develop optimal solutions to such basic problems as choosing where to look for food. So what's gone wrong here? If animals have accurate estimates of how much food is likely to be where -- however those estimates are learned -- then the rule of "[proportioning] their choices in accord with the relative expected rates" is the students' solution, not the rat's solution. The rule says to allocate your foraging time among the alternative locations in proportion to your estimate of the likely pay-off. That's what the students did. But the maximum-likelihood solution is to put all your chips on the option with the highest expected return -- what the rat did.

Did evolution screw up, then? No. In a situation of competition for resources, if everyone goes to the best feeding station, then that turns out not to be such a great choice after all. In that case, if you happen to be the only one who goes to the second-best place, you're in terrific shape. Of course, if lots of others have that idea too, then maybe you'd better check out the third-best. Overall, the best policy -- for you as an individual -- is to follow a strategy that says "allocate your foraging time probabilistically among the available alternatives, in proportion to your estimate of their profitability". At least, this is an evolutionarily stable strategy, "which if adopted by a population cannot be [successfully] invaded by any competing alternative strategy".

We often see a beautiful theory spoiled by an inconvenient eruption of fact. An honest investigator not only acknowledges this when it happens, but searches for such refutations, although no one should rejoice to find one. Here a good story is spoiled by a beautiful theory. That's a trade worth accepting cheerfully at any time.

This post is already too long, so I'll reserve for another day an account of how you can test this theory with a couple of loaves of stale bread and a flock of ducks. And then the really interesting part is how this same idea might help explain the emergence of linguistic norms and other shared cultural patterns. For a preview, if you're interested, you can take a look at a couple of versions of a talk I've given on this subject -- an html version from 2000, and a powerpoint version from 2005.

Posted by Mark Liberman at December 11, 2005 09:40 PM