September 09, 2006
Girls and boys and classroom noise
Here we go again -- yet another dissection of the misuse of science to make an ideological point about sex differences. If you're bored with this stuff, you can read the rest of this post for its information about the psychophysics of hearing, or for tips about how to concoct an effective argument by misrepresenting unrepresentative numbers.
We're back with Leonard Sax's book, "Why Gender Matters: What Parents and Teachers Need to Know about the Emerging Science of Sex Differences". The theme of this book is that that "Girls and boys play differently. They learn differently. They fight differently. They see the world differently. They hear differently." And as a result, they need sex-segregated education.
Sax's proposals deserve a hearing -- and they're getting one. David Brooks, in the New York Times, called Why Gender Matters "a lucid guide to male and female brain differences". A Time Magazine cover story said that "Until recently, there have been two groups of people: those who argue sex differences are innate and should be embraced and those who insist that they are learned and should be eliminated by changing the environment. Sax is one of the few in the middle -- convinced that boys and girls are innately different and that we must change the environment so differences don't become limitations." As an educational philosophy, this is plausible and interesting (though the devil, of course, is in the details).
But a very large part of the argument that Sax presents is based not on educational philosophy, nor on educational research, but rather on what Sax calls "the emerging science of sex differences". Sax has both a PhD and an MD, and he supports his position with extensive citations of results from neuroscience, psychophysics, cognitive psychology, social psychology and related areas. However, when I've followed up on the research mentioned in his text or cited in his end-notes, I've been shocked by the deep disconnect between the actual content of the research and the rhetorical use that Sax makes of it. Although I'm sympathetic to Sax's goals, this carelessness (or worse) leaves me worried about the competence and effectiveness of his movement's educational prescriptions.
This post presents another example of the disconnect between Sax's rhetoric and Sax's science. We're focusing on the "They hear differently" part of his theme, which I've examined earlier ("Leonard Sax on hearing"). In the argument we're going to discuss, Sax picks two unrepresentative numbers (from a set of 144 numbers in a published table) so as to exaggerate the point he wants to make. Then he claims that his selected numbers imply a difference of 10 to 1 or 100 to 1, whereas they actually imply a difference of about 1.4 to 1 on the relevant scale. And then he weaves the result, which deals with the difference between young women and middle-aged men, into an argument about how "Girls won't learn as well in a loud, noisy classroom ... [but] the rules are different when you're teaching boys."
Here's the passage in question (p. 18 of Chapter 2, "Female Brains, Male Brains"):
The difference in how girls and boys hear also has major implications for how you should talk to your children. I can't count the number of times a father has told me, "My daughter says I yell at her. I've never yelled at her. I just speak to her in a normal tone of voice and she says I'm yelling." If a forty-three-year-old man speaks in what he thinks is a "normal tone of voice" to a seventeen-year-old girl, that girl is going to experience his voice as being about ten times louder than what the man is hearing.18 He is yelling at her, but he doesn't realize it. The father and his daughter are experiencing the same sound in two different ways.
The gender difference in hearing also suggests different strategies for the classroom. [...] Girls won't learn as well in a loud, noisy classroom ... [but] the rules are different when you're teaching boys.
End-note 18 turns out to be this:
18. Actually, the girl is going to experience her father's voice as being more than 100 times louder in amplitude than what the father himself is experiencing. Corso (1959) found that the threshold for a 3-kHz tone for a 43-year-old man was 30.5 decibles [sic] (dB), while the threshold for a 3-kHz tone for an 18-year-old girl was 7.3 dB. That's a difference of 23.2 dB (30.5-7.3 = 23.2). A difference of 23.2 dB corresponds to more than a hundred-fold difference in the amplitude of the sound. If you're a little rusty on this, recall the definition of decibels (dB):
Sound in dB = 10 log [amplitude/reference]
23.2/10 = 2.32, so a 30-5 decibel sound has an amplitude that is 102.32 times louder, or > 100-fold louder, than a 7.3 dB sound.
These passages contain multiple examples of using "science" to mislead people. I'm going to focus on three of them: selection of unrepresentative values, misleading interpretation of values, and misleading transfer of results from one context to another. (There are some others, such as use of average values without considering variances, which I'll leave for another time.)
1. Selection of unrepresentative values.
Sax's cited threshold values come from a classic study: John F. Corso, "Age and Sex Differences in Pure-Tone Thresholds", The Journal of the Acoustical Society of America, 31(4), pp. 498-507 (1959). Corso measured how loud tones of different frequencies had to be for subjects to hear them, across a range of frequencies from 250 Hz to 8,000 Hz. He tested a large number of males and females of different ages from the students, faculty and staff at Penn State. He presents the results in multiple tables of values, providing means and standard deviations of thresholds for different ears of subjects of different ages and sexes, for sounds of different frequencies. He presents one set of tables is for his whole population of subjects, and other set of tables from a "screened" group from which he eliminated subjects who had abnormal amounts of hearing loss. You can see copies of three of these tables here, here, and here.
Corso's work established without any question that (on average) "women have more sensitive hearing than men". He also showed that "[f]or both men and women, there is a decrease in average hearing sensitivity with increasing age, and a progressive spreading of the loss from the higher to the lower frequencies. Men are more affected than women, with the hearing loss occurring at an earlier age and producing a greater degree of auditory impairment."
The question is, how much impairment is there, and what does it mean for perceived loudness levels in speech?
Corso's multiple tables contain hundreds of values. His Table 1 alone ("Summary of threshold data (SPL) by age groups, sex and ears for the original sample of subjects") offers 144 thresholds to choose from. Sax gives us two thresholds taken from this table: the threshold for a 3-kHz tone for a 43-year-old man was 30.5 decibles [sic] (dB), while the threshold for a 3-kHz tone for an 18-year-old girl was 7.3 dB.
Let's zero in on the slices of this table for the age ranges that Sax has chosen, which are 18- to 24-year-old females and 43- to 49-year-old males. I've added a central column with the threshold differences, and in an attempt to make the table easier to read, I've reproduced the standard deviations only for the right-ear thresholds:
| Frequency | Ear | 18-24 females | "Dad-Daughter" Difference |
43-49 males | ||
| mean | s.d. | mean | s.d. | |||
| 250 | R | 24.3 |
4.2 |
4.1 |
28.4 |
15.6 |
| L | 24.5 |
4.3 |
28.7 |
|||
| 500 | R | 11.0 |
4.2 |
1.5 |
12.5 |
14.0 |
| L | 9.1 |
2.1 |
11.2 |
|||
| 1000 | R | 5.7 |
4.3 |
4.4 |
10.1 |
13.4 |
| L | 4.2 |
6.2 |
11.4 |
|||
| 1500 | R | 5.3 |
4.6 |
9.0 |
14.3 |
12.8 |
| L | 4.5 |
11.9 |
16.4 |
|||
| 2000 | R | 5.5 |
5.4 |
8.9 |
14.4 |
11.5 |
| L | 4.4 |
14.5 |
18.9 |
|||
| 3000 | R | 7.5 |
6.3 |
19.4 |
26.9 |
18.5 |
| L | 7.3 |
23.2 |
30.5 |
|||
| 4000 | R | 11.1 |
5.8 |
23.8 |
34.9 |
18.0 |
| L | 9.5 |
28.1 |
37.6 |
|||
| 6000 | R | 21.4 |
6.9 |
20.8 |
42.2 |
21.4 |
| L | 21.1 |
28.5 |
49.6 |
|||
| 8000 | R | 17.1 |
6.0 |
18 |
35.1 |
20.5 |
| L | 22.3 |
19.7 |
42.0 |
|||
The two values that Sax has chosen, indicated in red in the table above, compare the left ears at 3 kHz. If instead he had chosen the right ear at 1500 Hz (which is the middle of the range of frequencies most important for speech -- the "telephone band" of 300 to 3200 Hz) he would have gotten a threshold difference of 9 dB rather than a difference of 23.2 dB. A more reasonable solution would be to weight the whole range of frequency and ear differences according to their likely contribution to the perception of loudness in speech. The energy in speech across frequencies follows a 1/F distribution, which means that speech is heavily weighted toward lower frequencies -- so that this approach would suggest a substantially lower estimate for the relevant overall threshold difference.
2. Misleading interpretation of values.
Whatever value we choose to represent the difference in thresholds, what does it mean about loudness perception? The threshold measure tells us about the level of the softest sound that you can hear -- how does this apply to your perception of relative loudness at moderate or higher sound levels? Sax claims in his text that "If a forty-three-year-old man speaks in what he thinks is a 'normal tone of voice' to a seventeen-year-old girl, that girl is going to experience his voice as being about ten times louder than what the man is hearing." In his end-note, he says that "Actually, the girl is going to experience her father's voice as being more than 100 times louder in amplitude than what the father himself is experiencing."
These statements are seriously mistaken. Even if we accept Sax's misleading selection of threshold values, the predicted difference in perceived loudness for the sound of an animated conversation would be about 1.4 to 1, not 10 to 1, much less 100 to 1. If we take the (more reasonable) estimate of a 5 to 10 dB difference instead of the unrepresentative 20-dB difference that Sax picks, the predicted difference in perceived loudness would be much smaller.
Here are the details...
The subjective dimension of loudness is measured in sones, where 1 sone is the perceived loudness of a pure tone of 1 KHz at 40 dB, and a doubling of subjective loudness is matched by a doubling of the loudness measure in sones. In general, the slope of the function relating objective sound level to perceived loudness is less than one, so that if you double the objective sound level (in dB), the perceived loudness (in sones) is less than doubled. And the slope decreases as the sounds get louder. As a result, elevated hearing thresholds (including those routinely associated with aging) cause a relative compression of perceived loudness levels, which increases with increasing sound levels.. This phenomenon is known as "loudness recruitment", and it's a significant problem for the design of hearing aids.
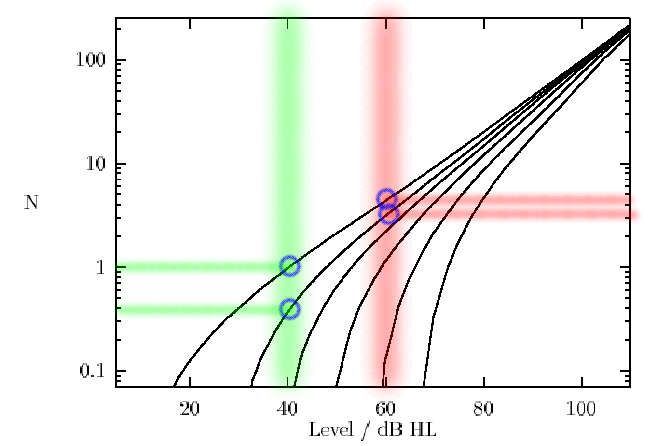
These effects are illustrated in a figure from chapter 7 of Stefan Launer, "Loudness Perception in Listeners with Sensorineural Hearing Loss" (1995), which shows the relationship between sound level in dB and perceived loudness in sones, for listeners with different thresholds:
Fig. 7.2: The loudness functions in units of sones are plotted versus stimulus levels with different thresholds EThQ as parameter. Note that the loudness functions grow at a higher rate when threshold EThQ is increased. EThQ = 10,30,40,50,60,70 dB, curves from left to right, respectively.
I've added vertical lines at sound levels of 40 dB and 60 dB, which correspond to the range of sound levels encountered in normal conversation. (Genuine "yelling" might get up over 80 dB, but as you'll see, this would just increase the effect I'm describing here.)
At each of these two objective sound levels, I've added two little blue circles, on the loudness functions corresponding to hearing thresholds of 10 dB and 30dB, which are fairly close to Sax's "daughter" and "father" thresholds, and two horizontal lines that map the points identified by those circles to the corresponding subjective level in sones.
Thus at a simulus level of 40 dB, the pseudo-daughter's loudness perception would be 1.0 sones, while the pseudo-dad's loudness perception would be 0.4 sones. At a stimulus level of 60 dB, the pseudo-daughter's loudness perception would be about 4.5 sones, while the pseudo-dad's perception would be about 3.2.
Thus even if there's a difference of 20 dB in hearing thresholds, the predicted difference in loudness perception over the range of normal conversational sound levels is predicted to range from 1.0/0.4 = 2.5-to-1 for soft conversation, to 4.5/3.2 = 1.4-to-1 for loud conversation. If we get up into the 80 dB range of serious yelling, the difference of perceptions will have narrowed almost to nothing.
So even if Sax's claim about the typical difference in hearing thresholds were correct, the difference in perceptions would not be 10 to 1, as he claims in the text, much less "more than 100-fold louder" as he claims in the footnote. Instead, it would be a difference of about 1.4-to-1 for moderately loud conversation, and progressively less as the sound intensity increases. If we re-do the calculation based on the overall amplitude spectrum of speech and the range of threshold values given in Corso's tables (which will result in a difference that is more like 5-10 dB rather than 20+ dB), the predicted difference in loudness perception will be negligible.
3. Misleading transfer of results from one context to another
Amid all this detail about the psychophysics of hearing, let's not lose sight of the point. This is supposed to be about the fact that "[g]irls and boys ... hear differently." But so far, we've been comparing women 18-24 years old to men 43-49 years old. This allows Sax to bring in an evocative anecdote about teenage girls who think that their fathers are "yelling" at them when their fathers think they're talking at a normal level (see "The emerging science of gendered yelling" for more discussion). But what about how girls and boys hear? Sax doesn't provide any scientific evidence to support his assertions about this -- or rather, the evidence that he cites is irrelevant or interpreted backwards. And Corso didn't test any subjects from the primary- or secondary-school years. But let's take a look at the most relevant comparison in his paper, namely the sex difference in hearing thresholds for 18-24-year-olds. As I understand it, the differences for school-age kids should be similar.
Here's the relevant slice from Corso's Table IV ("Summary of means and standard deviations combined for right and left ears of male and female subjects in the screened sample"):
| Frequency | Females 18-24 | Female-male difference |
Males 18-24 | ||
| Mean | s.d. | Mean | s.d. | ||
| 250 | 24.3 |
4.3 |
2.5 |
26.8 |
4.6 |
| 500 | 9.6 |
5.0 |
1.5 |
11.1 |
4.8 |
| 1000 | 4.8 |
4.5 |
1.1 |
5.9 |
4.4 |
| 1500 | 5.2 |
4.9 |
2.0 |
7.2 |
5.2 |
| 2000 | 4.7 |
4.6 |
3.0 |
7.7 |
6.2 |
| 3000 | 7.7 |
5.8 |
5.1 |
12.8 |
7.2 |
| 4000 | 10.1 |
5.4 |
3.9 |
14.0 |
8.6 |
| 6000 | 21.1 |
6.3 |
8.9 |
30.0 |
13.1 |
| 8000 | 19.4 |
8.4 |
8.2 |
27.6 |
14.0 |
I've stuck in a central column with the male-female differences in dB -- and I'll leave it as an exercise for the reader to look at the loudness-function plot given above, so as to verify that at classroom sound levels of 60-80 dB, the predicted average difference in female and male students' perceived loudness due to these average threshold differences will be around the thickness of the plotted black lines, if not less. [This is assuming a weighted average difference in thresholds of around 3 dB, translated into sones at a classroom noise level of about 70 dB.]
Girls and boys do hear differently -- but not by very much. If it's really true that "Girls won't learn as well in a loud, noisy classroom ... [but] the rules are different when you're teaching boys", it must be for some other reason than the (small) differences in their average hearing thresholds, which over the relevant range of frequencies is about 2 or 3 dB, representing a quarter to half a standard deviation, and at most a few percent average difference in loudness scaling.. And given how careless Sax is about interpreting his references on the psychophysics and neuroscience of hearing, I don't have much confidence that he has good evidence for sex differences in the educational effects of classroom noise.
Earlier Language Log posts on Leonard Sax and Why Gender Matters:
"David Brooks, cognitive neuroscientist" (6/12/2006)
"Are men emotional children?" (6/24/2006)
"Of rats and (wo)men" (8/19/2006)
"Leonard Sax on hearing" (8/22/2006)
"More on rats and men and women" (8/22/2006)
"The emerging science of gendered yelling" (9/5/2006)
[Update 5/29/2008 -- see Dr. Leonard Sax's response here, and some further discussion by me at
"Sax Q & A", 5/17/2008
"Liberman on Sax on Liberman on Sax on hearing", 5/19/2008
]
Posted by Mark Liberman at September 9, 2006 10:22 AM