Language Log

Conservation of (orthographic) gemination

Lauri Karttunen once remarked to me that Americans, who misspell his last name a lot, render it as "Kartunnen" more often than as "Kartunen". That is, rather than just omitting the doubled letter T, they substitute a doubled letter N instead. This is not a mistake that any native speaker of Finnish is likely to make,but non-Finns seem to remember that there's a double letter in there somewhere, even if they aren't very sure where it is.

I thought of this the other day, because in a post about Attila the Hun, in which the name "Attila" occurred a half a dozen times, I misspelled it once as "Atilla". I noticed the error and corrected it, even before Geoff Pullum did. But meanwhile, David Pesetsky had emailed me with important movie lore. He first copied my error, and then immediately correctly himself: "Did I really just spell Attila with one T and two L's? I do know better." Well, both of us do, but our pattern of typos still exhibited Lauri's hypothesized conversation of gemination.

Despite Lauri's many contributions, I feared that the name Karttunen would not occur often enough on the internet to check his intuition statistically. But Attila is another matter.

When I queried Google a few days ago, I got the following page counts:

String	Ghits
"atila the hun"	989
"attila the hun"	43,300
"atilla the hun"	9,400
"attilla the hun"	2,400

I didn't go any further with the issue then, but this evening I'm riding Amtrak from Washington to Philly, and so I have a few minutes to play with the numbers.

Arranging the counts in a 2x2 table, and giving the row and column sums as well as the overall total, we get:

	l	ll
t	989	9,400	10,389
tt	43,300	2.400	45,700
	44,289	11,800	56,089

One sensible way to view this set of outcomes is as the results of two independent choices, made every time the word is spelled: whether or not to double the T, and whether or not to double the L. After all, every one of the four possible outcomes occurs fairly often. This is the kind of model of typographical divergences -- whether caused by slips of fingers, slips of the brain, or wrong beliefs about what the right pattern is -- that underlies most spelling-correction algorithms.

In the case of the four spellings of Attila, we can represent the options as a finite automaton, as shown below:

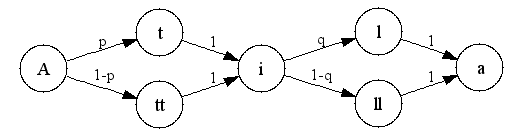
There are four possible paths from the start of this network (at the left) to the end (at the right). Leaving the initial "A", we can take the path with probability p that leads to a single "t", or the alternative path with probability 1-p that leads to a double "tt". There is another choice point after the "i", where we can head for the single "l" with probability q, or to the double "ll" with probability 1-q. In this simple model, the markovian (independence) assumption means that when we make the choice between "l" and "ll", we take no account at all of the choice that we previously made between "t" and "tt".

But are these two choices independent in fact? If Lauri was right about the "conservation of gemination", then the two choices are not being made independent of one another. Writers will be less likely to choose "ll" if they've chosen "tt", and more likely to choose "ll" if they've chosen "t".

There are several simple ways to get a sense of whether the independence assumption is working out. Maybe the easiest one is to note that in the model above, the predicted string probabilities for the four outcomes are

	l	ll
t	pq	p(1-q)
tt	(1-p)q	(1-p)(1-q)

This makes it easy to see that (if the model holds) the column-wise ratios of counts should be constant. In other words, if we call the 2x2 table of counts C, then C(1,1)/C(2,1) (i.e. atila/attila) should be pq/((1-p)q) = p/(1-p), while C(1,2)/C(2,2) (i.e. atilla/attilla) should be (p(1-q))/((1-p)(1-q)) = p/(1-p) also. We can check this easily: atila/attila is 989/43,300 = .023,while atilla/attilla is 9,400/2,400 = 3.9.

The same sort of thing applies if we look at the ratios row-wise: C(1,1)/C(1,2) (i.e. atila/atilla) should be pq/((p(1-q)) = q/(1-q), while C(2,1)/C(2,2) (i.e. attila/attilla) should be ((1-p)q)/((1-p)(1-q)), or q/(1-q) also. Checking this empirically, we find that atila/atilla is 989/9,400 = .105, while attila/attilla is 43,300/2,400 = 18.0.

Well, .023 seems very different from 3.9, while .105 seems very different from 18.0. But are they different enough for us to conclude that the independence assumption is wrong? or could these divergences plausibly have arisen by chance?

The exact test for this question is called "Fisher's Exact Test" (as discussed in mathworld, and in this course description for the 2x2 case). If we apply this test to the 2x2 table of "attila"-spelling data, it tells us that if the underlying process really involved two independent choices, the observed counts would be this far from the predictions with p = < 2.2e-16, or roughly 1 in 500 quadrillion times. In other words, the choices are not being made independently!

The direction of the deviations from the predictions also confirms Lauri's hypothesis -- writers have a strong tendency to prefer exactly one double letter in the sequence, even though zero and two do occur. Given that the two-independent-choices model is obviously wrong, there are other questions we'd like to ask about what is right. But with only four numbers to work with, there are too many hypotheses in this particular case, and not enough data to constrain them very tightly.

However, there's a lot of information out there on the net, in principle, about what kinds of spelling alternatives do occur, and what their co-occurrence patterns look like. The key problem is how to tell that a given string at a given point in a text is actually an attempt to spell some specified word-form. We've solved that problem here by looking for patterns like "a[t]+i[l]+a the hun" (not that Google will let us use a pattern like that directly, alas). In other cases, we would have to find some method for determining the intended lemma and morphological form for a given (possibly misspelled) string in context. This is not impossible but the general case is certainly not solved, or spelling correction programs would be much better than they are.

[Update: I was completely wrong about the possibility of checking this idea with web counts of the name Karttunen and its variants. We have
Karttunen 57,500
Kartunnen 3,330
Karttunnen 156
Kartunen 628
or in tabular form

	n	nn
t	628	3,330
tt	57,500	156

There is a small problem: many of these are actually valid spellings of other people's names (even if historically derived from spelling errors at Ellis Island or wherever), rather than misspellings of Karttunen. Still, the result also supports Lauri's hypothesis, and I have no doubt that it would continue to do so if the data were cleaned up.]

Posted by Mark Liberman at March 29, 2004 12:58 AM