Language Log

Music of the spheres -- and everything else

I've been working hard all day on non-bloggery -- letters of recommendation, grant proposals, project planning, laundry -- and so I'm going to indulge myself in a small rant about the popular presentation of astronomy. I'll get to a linguistic hook at the end.

Last year, it was "outbursts from a giant black hole" in the Perseus cluster at a "frequency ... equivalent to a B flat, 57 octaves below middle C". Now, according to an article by Dennis Overbye in the August 2 NYT, "another group of astronomers has discovered waves from another massive black hole spreading outward from the center of a galaxy known as M87". This one is "a little more than an octave higher than the Perseus black hole", and "a little rougher and less pure", sort of "like the cannons in the '1812 Overture'".

Give me a break. I'm not going to be as hard on Overbye as Geoff Pullum was, but I can't let this go by without a comment.

The universe is full of pitches, rhythms, periodicities at all scales of time and space. You can express any repetitive process as a musical tone if you want to. For example, you might pull up a sequence from the Tour de France, and find that Lance Armstrong is pedaling at a pitch of D, about 7 octaves below middle C. But except for a narrow range of frequencies of variation in air pressure, this translation into musical tone classes is irrelevant foolishness -- what you should really say is that Lance is pedaling at 140 cycles per minute.

Here's another example.

Because of interest in the southern oscillation, it's possible to find online a table of Monthly Mean Sea Level Pressure, measured at Tahiti, from 1876 to the present date. We can take this time series and look at its spectral content (I used the wonderful, free R statistics system):

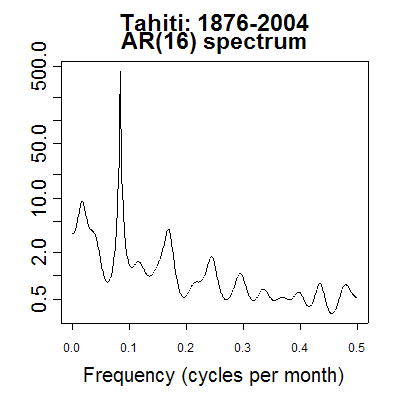
If we translate 'cycles per month' into 'cycles per year' we find that the dominant frequency in the long-term variation of (monthly average) barometric pressure measured in Tahiti is -- big surprise! -- exactly one cycle per year. We have a name for this "pitch" -- it's called "the seasons".

Alternatively, we could translate this frequency into cycles per second, and say (truthfully!) that the seasons are a very, very deep tone. Specifically, the air pressure variation associated with the seasons is a pitch near C#, about 33 octaves below middle C. This is the result of a trivial calculation:

Seconds per year = 365.25*24*60*60 = 31,557,600
One cycle per year, in cycles per second = 1/31,557,600 = 3.168809e-08 Hz
(1/31,557,600)*2^33 = 272.1986

So 272.1986 is the frequency in Hz. of the seasons (one cycle per year), shifted up in pitch by 33 octaves.

Middle C is nine semitones down from concert A at 440 Hz. -- that's 440/(2^(9/12)) = 261.6256 on an equally tempered scale. The C# one semitone up is 440/(2^(8/12)) = 277.1826 Hz.

So if I didn't embarrass myself by making a mistake in arithmetic, the seasons are pretty close to C# -- a mere 1.8% flat, less than a quarter tone -- about 33 octaves below middle C.

But does all this really tell us something that we didn't already know? On the contrary, it takes something very simple and obvious -- that the seasons run on a yearly cycle -- and expresses it in two fancy, mysterious and completely unhelpful disguises. We first disguised the seasons as a spectral peak at 3.168809e-08 Hz (about 32 nanohertz), and then as a musical tone near C# 33 octaves below middle C.

Why do journalists -- and scientists -- fall into this nonsense for intergalactic gas clouds, but not for weather patterns or bicycle pedaling or political speeches? I suppose it's partly the old meme of the "music of the spheres", and partly the fact that intergalactic gas is outside of everyone's ordinary experience, so it's not so obvious how dumb the calculation is.

In fact the spacing of the Perseus Cluster pressure waves -- B flat, 57 octaves below middle C -- corresponds to a frequency of (233.0819/(2^57)) = 1.617330e-15 cycles per second, or (233.0819/(2^57))*365.25*24*60*60 = 5.103907e-08 cycles per year, or about 19,592,833 years per cycle.

In other words, one wave front passes by about every 19 and a half million years. (Or maybe half that, depending on which octave the "pitch" is really in).

Do you feel enlightened, knowing that this is close to a B flat?

Music of the spheres? Music of the con artists, if you ask me. But maybe we linguists should learn something about public relations from these guys. Perhaps I should offer Dennis Overbye a scoop -- oh, say, that new measurements of George Bush's stump speech shows a syllabic frequency almost exactly 6 octaves below middle C. Whereas John Kerry's speeches are in the syllabic key of... well, you get the idea.

The fact is, it might be interesting to look at political discourse in terms of simple measurements of speech rate, pitch range and so on. But translating those measurements into musical tone classes would be obfuscation or worse.

[To prevent misunderstanding, let me make it clear that I haven't actually measured the average syllabic rate in the current stump speeches of any national candidates. But I very easily could -- Dennis, are you reading this?]

 

Posted by Mark Liberman at August 5, 2004 08:15 PM