April 20, 2005
(Mis)Informing Science
Jeff Erickson at Ernie's 3D Pancakes has an extensive review and discussion of the SCIgen affair, in which three MIT grad students got a randomly-generated paper accepted at one of the IIIS/SCI spamferences, as Jeff calls them. Jeff's post features an analysis of the response by the president of IIIS, Nagib Callaos, which Jeff calls a "mindboggling rambling rationalization".
Against this background, I thought I'd take a look at Prof. Callaos' own scholarship. When I checked a couple of days ago, Google Scholar had 33 hits for {Nagib Callaos}, just one of which was a link to a paper by Prof. Callaos in person, rather than a reference to his role as an editor of conference proceedings: Nagib Callaos and Belkis Callaos, "Toward a Systemic Notion of Information: Practical Consequences", Informing Science, 5(1) 2002. This paper has got some mindboggling properties of its own, epitomized by its observation that "[one] bit is the minimum information that a systems [sic] of two states can provide".
It's worth looking at the paper in a bit more detail, as a window into a curious quasi-technical demimonde.
The paper begins:
The meaning of “information systems” has been growing in diversity and complexity. Several authors have pointed out this fact, described the phenomena and tried to bring some order to the perceived chaos in the field. Cohen (1997, 1999, 2000), for example, after describing the attacks on the Information Systems (IS) field, for “its lack of tradition and focus” and the “misunderstandings of the nature of Information Systems,” examines “the limitations of existing frameworks for defining IS” and reconceptualizes Information Systems and tries “to demonstrate that it has evolved to be part on an emerging discipline of fields, Informing Science” (Cohen, 2000). Our objective in this paper is to participate in the process of conceptualization and re-conceptualization required in the area of Information Systems and in Cohen’s proposed Informing Science. We will try to do that making a first step in the description of a systemic notion of information, by identifying, first, the meaning of information. ...
Let's pass over the authors' discussion of what they call "The Subjective Conception of Information" and get to the section on "The Concept of Information as Objective Form or Order", which begins
Lately, an increasing number of authors are showing an objectivist bias in their conception of the notion of “information”. Shannon’s definition of information is at the roots of this perspective, and information technologies authors provided its strong impulse. Shannon, in his 1938 paper, "A Mathematical Theory of Communication," proposed the use of binary digits for coding information. ...
Shannon's paper was published in 1948, not 1938 (specifically, it was originally published in two parts: The Bell System Technical Journal, Vol. 27, pp. 379-423, 623-656, July, October 1948). Am I betraying my "objectivist bias" by fussing about the actual date? In any case, Shannon 1948 is not in the Callaos' paper's bibliography, despite being cited and discussed at some length.
Perhaps this bibliographic omission is an honest one -- at least, Callaos & Callaos seem confused to me about the "objectivist" ideas that they are rejecting, although I'm no kind of expert on information theory. They explain that "the information expected value of an n states system" is given by the equation (image copied from their paper):
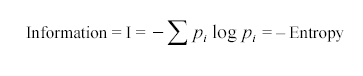
The core formula is correct. The equation given in Shannon 1948 is
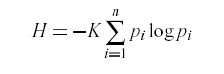
where K is a positive constant. But nothing is lost if K is set to 1 -- as Shannon explains, "the constant K merely amounts to a choice of a unit of measure", and Shannon also uses the equation without the constant, as we'll see below.
However, it's unexpected for Callaos & Callaos to equate this formula to "–Entropy", since Shannon's formula defines entropy, not negative entropy. The reason for the minus sign in Shannon's formula is that the p's here are probabilities, positive quantities between 0 and 1, whose logs are therefore all negative. (Well, non-positive, allowing for the case of only one option with p=1.) Without the minus sign, the sum would always be less than or equal to zero.
At first I thought that the minus sign in Callaos & Callaos' "–Entropy" was just a typographical error. But no, they go through the case of what they call a "two states system" in detail, concluding that the "minimum information" in this case is obtained when "p1 = p2 = 1/2",
And, if the logarithmic base is 2, then I = log22 = 1, which is the definition of "bit", i.e. a bit is the minimum information that a systems [sic] of two states can provide, or the information that could be provided by a 2 states systems [sic] with maximum entropy.
This seems deeply confused. One bit is the maximum quantity of information that can be provided by a choice between two alternatives, not the minimum. Shannon equated his quantity H directly with Boltzmann's entropy, and described entropy as "a reasonable measure of choice or information", not as a measure of the opposite of information:
Quantities of the form H= –Σ pi log pi (the constant K merely amounts to a choice of unit of measure) play a central role in information theory as measures of information, choice and uncertainty. The form of H will be recognized as that of entropy as defined in certain formulations of statistical mechanics where pi is the probability of a system being in cell i of its phase space. H is then, for example, the H in Boltzmann’s famous H theorem. We shall call H= –Σ pi log pi the entropy of the set of probabilities p1,...,pn. If x is a chance variable we will write H(x) for its entropy; thus x is not an argument of a function but a label of a number, to differentiate it from H(y) say, the entropy of the chance variable y.
How did Callaos & Callaos get this backwards? A clue is provided by a passage later in their paper:
Shannon’s Theory provided the grounds for a strong support to the objectivist position, where information is conceived as completely independent from their senders and receivers, and as a neutral reflection of real world structure or order. The identification of information with negative entropy, or negentropy, made by Shannon, gave the foundation of the increasing emphasis in the objectivist conception of information. Shannon found out that his equation was isomorphic with Boltzmann’s equation of entropy. So, equating both of them, he equalized information to negative entropy. This made some sense, because since entropy is conceived as disorder, negative entropy and information (its mathematical isomorphic) might be both seen as order. Then, anyone who conceives an independent order in the Universe would accept that information, its ‘synonym’, is independent, from any subject. This explains the increasing number of authors endorsing the objectivist position.
This passage seems to me to suffer from several basic confusions, which point to a sort of coherent pattern of error consistent with the earlier oddities in the paper.
Shannon's monograph was entitled "A Mathematical Theory of Communication", not "A Mathematical Theory of Real World Structure" or "A Mathematical Theory of Independent Order in the Universe". His theory is all about senders and receivers and communications channels. It does assume that we can tell whether the message received is the same as the message sent, and it offers a way of thinking about what happens to messages in noisy channels that are independent of both senders and receivers. But it applies just as well to messages whose content is false or undecidable as it does as to true ones. And to the extent that it's used for modeling conceptions of states of the world, as it is for instance in research on perception, this is done by casting the objective world in the role of the sender of a message.
The term "negentropy" was apparently coined by Schrödinger, in his 1944 book "What is Life?" (which apparently inspired James Watson's DNA research):
It is by avoiding the rapid decay into the inert state of `equilibrium' that an organism appears so enigmatic....What an organism feeds upon is negative entropy.
The wikipeida stub for negentropy says that
Schrödinger introduced that term when explaining that a living system exports entropy in order to maintain its own entropy at a low level. By using the term "Negentropy", he could express this fact in a more "positive" way: A living system imports negentropy and stores it.
Schrödinger also apparently suggested that "negative entropy" is something like "free energy". To understand what Schrödinger might have been getting at, and its relations to (the later development of) information theory, look at Tim Thompson's What is Entropy? page (especially his equations 3, 4 and 5). For some thoughts on difficulties with a simple-minded "entropy = disorder" equivalence, see Doug Craigen's summary, and his longer discussion of the same point.
So now I think I see what has happened. Callaos & Callaos start out thinking in terms of rather vague metaphorical relationships like "entropy is disorder" and "information is order", which predispose them to see entropy and information as opposites. Then they trip over the fact that in themodynamics, entropy is sometimes expressed in terms of the number of states of a system, rather than the probabilities of those states. Thus the equation carved on Boltzmann's tomb is
S = k log W
where S is entropy and W is the total number of microstates available to the system. Obviously in this case, W is a large positive quantity, and so log W is also positive. If all the states are equally probable, then the probability of each is 1/W. Since log(1/W) = –log(W), Boltzmann's tomb equation is equivalent to
S = –k log 1/W
and this is the form in which Shannon adopted it, since that form generalizes suitably to the case where the probabilities are not uniform.
Finally, this misunderstanding apparently resonated for Callaos & Callaos with some exposure to Schrödinger's idea of "negative entropy" as the essential stuff of life.
So, we start with a fuzzy conception that "entropy is disorder, information is order"; we add the existence of the term negentropy for "negative entropy", identified by Schrödinger as "what an organism feeds upon" (aha! life feeds on information!); we mix in a confusion over log W vs. –log 1/W ... and hey presto, we've apparently got a couple of deeply confused partisans of "informing science".
If this stuff were in a paper submitted by an undergraduate in a survey course I was teaching, this is the point at which I'd feel like I was starting to earn my salary. I've found a point of significant confusion and a hypothesis about its origin, and now I can sit down with the student and help them on the way to a clearer and more useful understanding of some basic and important ideas. I've also learned something myself (since the Schrödinger "negentropy" business was new to me).
However, according to the biographical sketches given at the end of the cited paper, the authors have been teaching for 32 and 25 years, respectively, on topics including "Informations Systems", "Operations Research", "Software Engineering" and so forth. The first author is president of the Venezuelan chapter of the IEEE/Computer Society. And the two authors are president and vice-president, respectively, of the International Institute of Informatics and Systematics (IIIS), the sponsor of the "spamferences" that started this whole discussion. In the face of these facts, I concur with Prof. Nagib Callaos in "having a huge sadneess".
[P.S. There are a number of other curious points in the cited Callaos & Callaos paper. For example, the biosketch for Nagib Callaos at the end of the paper tells us that
The core of most of his research is based on the Mathematical Solution to the Voter Paradox (or Condorcet Paradox) he discovered in his Ph. D. Dissertation, in opposition to Nobel Prize Kenneth Arrows [sic] who gave a mathematical proof (his Impossibility Theorem) of the impossibility to find a solution to the Voter Paradox. Professor Callaos showed, in his dissertation, several inconsistencies in Arrows’ axioms.
I'll leave it to someone else to track this one down.]
Posted by Mark Liberman at April 20, 2005 12:59 PM