December 02, 2005
The long tail: in which Gauss is not mocked, but TWiTs (and dictionaries) are
This all started a couple of weeks ago, when I listened to the podcast TWiT 30: Live from the Podcast Expo. TWiT stands for "This Week in Tech" (motto: "Your first podcast of the week is the last word in tech"). Here tech really means something like "California IT-industry gossip", but it's a fun show, full of good-natured geekoid banter, and I listen to it regularly. So I was shocked to discover that neither host Leo Laporte nor any of the other TWiTs has apparently ever learned any statistics. At least, none of them knows the sense of the word tail as (in the words of the OED) "An extremity of a curve, esp. that of a frequency distribution, as it approaches the horizontal axis of a graph; the part of a distribution that this represents".
Here's the evidence, in the form of some transcription fragments from the show. (There's a lot of what a social psychologist might call "co-construction of discourse", i.e. everybody talking at once, so the sequencing is approximate and some of the attributions may be wrong.)
Leo Laporte introduces one of the guests:
| Leo Laporte: | uh to begin kind of our- our round table of podcasters, Digital Bill from uh The Wizards of Technology, an old friend, and a great friend, and wearing a kilt in honor of Patrick Norton. |
Leo and Bill geek out for a while about microphone brands and model numbers -- Leo is excited about his new Heil PR-40, designed by "the former sound guy for the Grateful Dead", which was his prize for winning the People's Choice podcast award. (I'm using the pound sign # to indicate interruption points.)
| Digital Bill: | The question will be, can it happen again? |
| Leo Laporte: | Never. You know, I- I- I'm firmly of the opinion that the tech podcasts are on top now because that's who can get # podcasts. |
| Digital Bill: | The tech audience. |
| Doug Kaye: | Right. |
| Leo Laporte: | But I think by this time next year, it'll be- I hope it'll be a mainstream audience, don't you think, Bill? # I mean uh |
| Digital Bill: | Yeah, I- I- I do, I- I mean, We've been walking around and th- the thing that was always amazing to me is how many people come up to us a- you know as a tech podcast, and they're like "well it's- it's Wizards of Technology, we're not quite used to that", but some of the guys that came up and talked to us are people who have their own podcasts, uh the RaiderCast, uh the guy that has a podcast about didgeridoos, right, the Australian # instrument. |
| Leo Laporte: | I'd love that. [Begins imitating a didgeridoo...] |
Note that for Digital Bill, "mainstream audience" apparently means "people who are not interested in technology", including for example those who are interested in podcastsabout didgeridoos.
| Digital Bill: | He says he kn- he knows- he knows both of the guys in- in San Francisco that play them, and- but |
| Leo Laporte: | It's a small community but powerful. |
| Digital Bill: | they're- they're way out on the long tail, right, these are the guys who are but- but there's an interest for that, and no matter what you have to talk about, in podcasting, you have uh- whatever your passion is- |
| Leo Laporte: | There's somebody # to listen. |
| Digital Bill: | somebody's gonna want to listen, because you're not the only person that likes digeridoos, there are other people that do. |
There's some back-and-forth with Doug Kaye (of IT Conversations) about podcasts about knitting, and then Leo picks up an earlier thread:
| Leo Laporte: | So uh you said something th- that I keep hearing at this conference, Digital Bill, and I want to know what the hell it means: "long tail". |
| Digital Bill: | Oh, the "long tail". I don't know- |
| Leo Laporte: | Everybody's talking about the frickin "long tail". |
| Digital Bill: | Yeah. |
| Leo Laporte: | Is that the # word of the week? I don't- |
| Doug Kaye: | You don't have one? |
| Digital Bill: | ((I'll check: no.)) I had mine removed, actually, it doesn't look good with the kilt. |
| Leo Laporte: | You still have the bump, though, I understand. |
| Digital Bill: | You noticed that? |
| Leo Laporte: | Yeah. |
| Digital Bill: | Okay. |
| Doug Kaye: | [significantly] Okay... |
After this homoerotic interlude, Digital Bill takes up the challenge of explaining the "long tail":
| Digital Bill: | The- the long tail is the part of- of consumable stuff, I forg- you can probably explain this better than me, Doug, but it's- it's you know, there's an initial high-end of # demand |
| Doug Kaye: | That's the early adopters. |
| Digital Bill: | ...the early adopters, you know, they're the first per- people to jump on to any- any # new thing. |
| Leo Laporte: | So we're the fat part of the tail. |
| Digital Bill: | This- this # whole... |
| Leo Laporte: | The fat head. |
| Digital Bill: | ...this- this whole audience is- uh are early # adopters. |
| Leo Laporte: | So it's kind of like a spermatozoa? |
| Doug Kaye: | On the leading edge. |
| Digital Bill: | Uh it could be like that. And then i- it- you know that- that demand tapers off in kind of this uh you know tail-shaped uh pattern, but uh I think Ama- Amazon were the ones who kind of discovered it through all their data mining and so forth is that they have the- a larger percentage of their total sales volume come from those small demand things, but there's just so many of # them out there, |
| Leo Laporte: | Aaah. |
| Digital Bill: | that- that it- it- it adds up to such a large volume, they're- |
The TWiTs then agree that all this has something to do with the internet and business models and stuff:
| Leo Laporte: | So the long tail really is important in an e- in a- in internet sense, when you have massive # numbers. |
| Digital Bill: | Well and remember that we all decided that the internet is now not a fad. for a l- remember the internet itself was originally bl- oh, that's just- that's just a fad, yeah? |
| Doug Kaye: | No and I- I- I think also that the uh uh Netflix is- is a perfect example of someone # who's taking full advantage of the long tail, |
| Digital Bill: | Yeah, Netflix is one too, yeah. |
| Doug Kaye: | ...where most- a lot of times what you think of is, I can go get that at Netflix, wh- I can't get that anywhere else. |
| Leo Laporte: | Right. |
| Doug Kaye: | So a lot of their business- their whole business model is based on the ability to do that. |
| Leo Laporte: | So if Amazon didn't have every book, or Netflix didn't have every movie, there'd be no long tail. |
| Doug Kaye: | Yeah, I mean it really came fr- it was uh coined by Chris Anderson at Wired Magazine and he did the first article, and he's got a book coming out about the long tail, which I # ((believe it)) |
| Digital Bill: | How to have a long tail. |
| Doug Kaye: | Yeah, exactly. But it was- it was literally Amazon was his first case, and it said ... |
Well, you can read Chris Anderson's article for yourself. And if you search Google Images for "long tail", you'll find lots of copies of pictures like this one, which will give you an idea of what this is all about. It may also suggest why the TWiTs (who have probably seen slides like this) have gotten all confused about the relationship of the "long tail" to their beloved early adopters: for books and movies, most sales are soon after release.
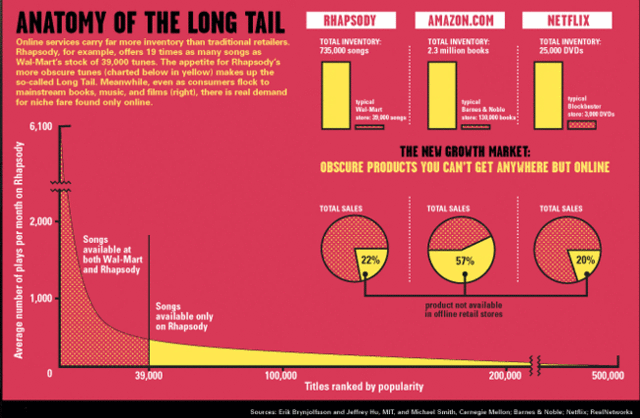
However, Anderson's "long tail" is not about those who are not early adopters, any more than "mainstream audiences" are those who are interested in didgeridoos and knitting. In fact, the usage doesn't come from any of the temporal senses of tail, such as (from the OED again) "The terminal or concluding part of anything, as of a text, word, or sentence, of a period of time, or something occupying time, as a storm, shower, drought, etc.", or "The rear-end of an army or marching column, of a procession, etc.". Instead, the source is the statistical sense quoted earlier: "An extremity of a curve, esp. that of a frequency distribution, as it approaches the horizontal axis of a graph; the part of a distribution that this represents". The OED's first citation for this sense comes from Karl Pearson more than a century ago:
1895 K. PEARSON in Phil. Trans. R. Soc. A. CLXXXVI. 397 We require to have the ‘tail’ as carefully recorded as the body of statistics. Unfortunately the practical collectors of statistics often..proceed by a method of ‘lumping together’ at the extremes of their statistical series.
What makes a statistical tail "long"? To understand this, we've got to start with the Central Limit Theorem, which says that the sum of many independent random variables with finite variance will be approximately gaussian, i.e. "normal", with the approximation improving as the number of variables increases. This might seem like an obscure idea, as remote from internet marketing buzz as didgeridoos are from mainstream media. But in fact it's a major theme of 20th-century science, and exactly the sort of thing that I would have thought that a bunch of tech geeks would be steeped in.
To give a sense of the status of the CLT, I'll quote a bit from Cosma Shalizi's lovely weblog post of 10/28/2005, "Gauss is not mocked".
Let me turn the microphone over to Francis Galton (as quoted in Ian Hacking's The Taming of Chance):
I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by `the law of error.' A savage, if could understand it, would worship it as a god. It reigns with severity in complete self-effacement amidst the wildest confusion. The huger the mob and the greater the anarchy the more perfect its sway. Let a large sample of chaotic elements be taken and marshalled in order of their magnitudes, and then, however wildly irregular they appeared, an unexpected and most beautiful form of regularity proves to have been present all along.
As Hacking notes, on further consideration Galton was even more impressed by the central limit theorem, and accordingly replaced the sentence about savages with "The law would have been personified by the Greeks and deified, if they had known of it." Whether deified by Hellenes or savages, however, the CLT has a message for those doing data analysis, and the message is:
Thou shalt have no other distribution before me, for I am a jealous limit theorem.
When I took probability and statistics as an undergraduate in 1966 or so, we spent the whole first semester deriving several different versions of the Central Limit Theorem in several different ways from several different sets of axioms. It was strangely like medieval schoolboys being drilled in Aquinas' five proofs of the existence of God. Only in the second semester, after a suitable reverence for the CLT had been impressed on us, did we actually encounter any of the apparatus of 20th-century inferential statistics that is based on it.
When I got to Bell Labs in 1975, it was refreshing to be exposed to the counter-cultural resonances of John Tukey's skeptical take on the bad effects of (often untested) assumption of normality. This started (I think) with his much-cited 1960 paper "A Survey of Sampling From Contaminated Distributions" (in Contributions to Probability and Statistics, Olkin, ed.). Tukey's 1977 books Exploratory Data Analysis and Data Analysis and Regression sold this idea to a wider audience. A key point was that real-world distributions often have "longer tails" than the gaussian approximation characterized by sample estimates of mean and variance. In other words, you find a much larger proportion of your observations further away from the commonest range of values than this fitted "normal" approximation predicts. Tukey argued that this fact can often result in errors of statistical inference.
The "long tail" might arise because the real data distribution has tails that don't decay exponentially, the way the gaussian or normal distribution's tails do, for example if the real underlying distribution is a 1/F or power-law distribution. However, as Cosma's post suggest, it can be for other reasons as well. Thus Tukey's original 1960 paper dealt with the "contaminated" normal distribution, which is a mixture of two gaussians, one with a much higher variance than the other.
In the 1970s and 1980s, statisticians and other became very interested in distributions with "long tails". You can find thousands of papers like Montroll, Elliott W. and Shlesinger, Michael F. "On $1/f$ noise and other distributions with long tails", Proc. Nat. Acad. Sci. U.S.A. 79 (1982). As that particular title suggests, the attention generated by Turkey's concern for robust statistical estimation was soon turbo-charged by popular interest in fractals, self-similar distributions, Zipf's Law, Pareto's Law, and similar themes of 1980s math-geek culture. Perhaps the apotheosis of this buzz was Per Bak's (apparently mistaken) 1988 argument that 1/F noise is a sign of "self-organized criticality", which is turn was argued to be How Nature Works. By 1988, the 1960s' focus on admitting data points far from the norm had been incorporated into the mainstream, in applied math as in the society at large.
So by the time the internet came along, "long tailed" distributions (whether 1/F or not) were part of the standard conceptual toolkit of elementary applied mathematics, and the term "long tail" was widely used in this context. Thus in Bernardo A. Huberman, Lada A. Adamic's paper, "Growth dynamics of the World-Wide Web" (Nature 401(9), September 1999), we find
"But although it is skewed and has a long tail, the log-normal distribution is not a power-law one."
As Amazon and other internet retailers have demonstrated, long-tailed distributions of consumer demand -- in the sense of distributions where a large fraction of the probability mass is in the tail -- are a Good Thing for companies that can cope efficiently with orders for the very large array of books, CDs, movies and so on that are not among the top sellers. That's where Chris Anderson's Wired article "The Long Tail" starts. He claims that a much bigger fraction of the (potential sales) mass than you might think is out in the tails of the distribution of consumer demand, and he turns the phrase "long tail" into a bugle call for the redesign of post-modern life:
You can find everything out there on the Long Tail. ... There are niches by the thousands, genre within genre within genre ...
And the cultural benefit of all of this is much more diversity, reversing the blanding effects of a century of distribution scarcity and ending the tyranny of the hit.
Such is the power of the Long Tail. Its time has come.
I have no doubt that Gauss and Turing are raising a glass or two with John Tukey, in celebration of this development.
Meanwhile, the "tail of a distribution" sense of tail is not only news to the TWiTs, it's missing entirely from the American Heritage Dictionary, from Merriam-Webster Online, and from Encarta. It's even missing from Merriam-Webster's Unabridged (3rd Edition), which gives no fewer than 21 other senses, including obscure ones like "a sprout of barley" or "the exposed lower end of a slate, tile or rafter". So now that the time of the Long Tail has come, perhaps its terminological parent should be admitted into dictionaries other than the OED?
Posted by Mark Liberman at December 2, 2005 09:05 AM