March 21, 2007
Spice Names
Yesterday, Carl Manaster wrote to Geoff Nunberg:
I've noticed a few times just how over-represented the letter "C" is as the initial letter of spice names. Something like 1/4 of the spices in my rack start with "C" and of course there are 25 other perfectly good letters they could start with. And I got to wondering why, and I googled, and came up with bupkis. This strikes me as something you may already know the answer to, or, if you don't, something you would enjoy tracking down. If you have or come up with an answer, I'd be really interested to hear it.
And Geoff forwarded the note to the rest of us Language Loggers, and Arnold Zwicky suggested that I try to make this the basis of a little statistics lesson. So here goes.
First, what proportion of spice names start with the letter 'c'? I don't know what's in Carl's spice rack, but there's a list of 40 "Herbs & Spices" on the McCormick company's web site: Allspice, Ancho Chile, Anise, Basil, Bay Leaves, Black Pepper, Caraway Seed, Cardamom, Celery Seed, Chervil, Chipotle Chile, Chives, Cilantro, Cinnamon, Cloves, Coriander, Cumin, Dill, Fennel, Ginger, Mace, Marjoram, Mint, Mustard, Nutmeg, Oregano, Paprika, Parsley, Poppy Seed, Red Pepper, Rosemary, Saffron, Sage, Savory, Sesame Seed, Tarragon, Thyme, Turmeric, Vanilla, White Pepper.
Of these, I reckon that 22 (Allspice, Anise, Black Pepper, Caraway Seed, Cardamom, Celery Seed, Cinnamon, Cloves, Coriander, Cumin, Ginger, Mace, Mustard, Nutmeg, Paprika, Poppy Seed, Red Pepper, Saffron, Sesame Seed, Turmeric, Vanilla and White Pepper) are spices rather than herbs. 7 out of 22 start with the letter 'c', or 31.8%.
How likely is this to happen by chance? Well, suppose that we were picking English nouns at random as spice names. Out of 26,003 nouns in the CELEX2 English lexicon, there are 2,713 whose spelling starts with the letter 'c', or 10.4%. If we picked 22 nouns at random, how likely is it that 7 or more of them would start with 'c'?
These days, the most straightforward way to answer a question like this is to do a Monte Carlo simulation. This is easy to do, e.g. in the (free software) statistics language R:
Nitems <- 22
Frac <- 2713/26003
Num <- 100000
counts <- mat.or.vec(23,1)
for (i in 1:Num) {
n <- sum(runif(Nitems)<Frac)+1
counts[n] <- counts[n]+1
}
propgreq <- rev(cumsum(rev(counts)))/Num
The proportion of runs with 7 or more C-initial words (propgreq[8] after running the code above) is about .005, i.e. one time in 200.
Here's a couple of relevant plots:
png(filename="SpiceNames%d.png", width=700, height=700)
plot(0:10, counts[1:11],
xlab="Number of C-initial words (out of 22 words)",
ylab="Count (out of 100,000)",
main="Random selection of 22 nouns from English CELEX2", type="b")
plot(0:10, propgreq[1:11],
xlab="X or more (of 22) C-initial words",
ylab="Proportion of trials",
main="Random selection of 22 nouns from English CELEX2", type="b")
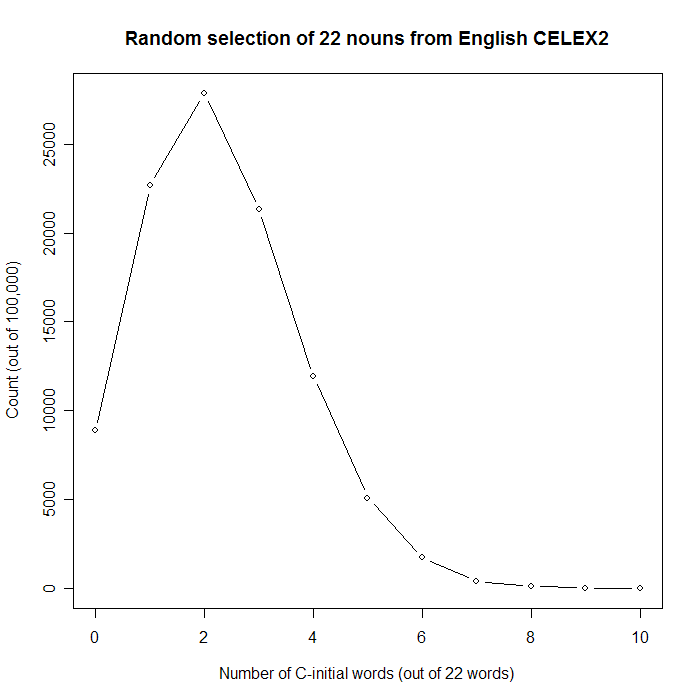
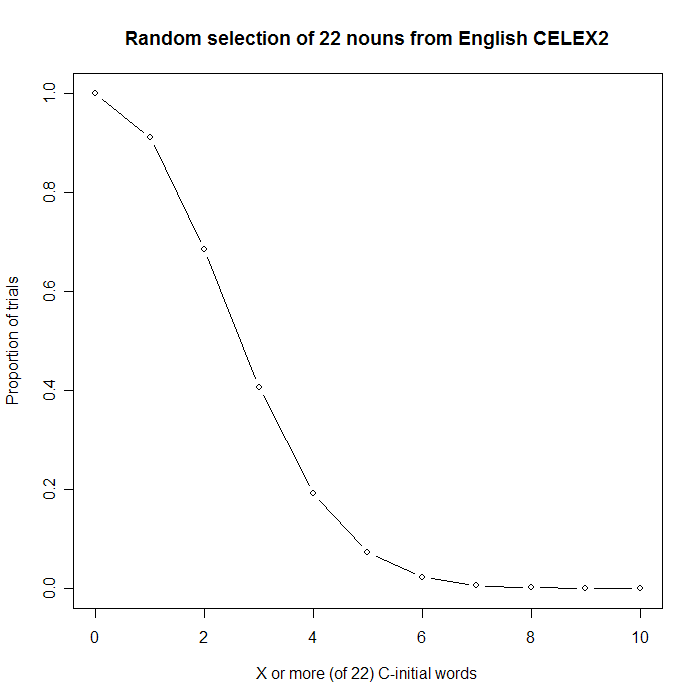
So, we can be pretty sure that spice names are richer in initial 'c' than expected on the basis of the English noun vocabulary as a whole.
In conversation around the virtual water cooler at Language Log Plaza, Dan Jurafsky observed:
Assuming that c is indeed statistically over-represented compared to its distribution in english, i assume it's because spice names pass through multiple languages, and
a) the distribution is different in those languages
b) the borrowing process accidentally funneled through some many-to-one-mappings that may increase the proportion of c's (some of this just from a quick check of the dictionary, probably some errors here):
- lots of spice names come from arabic/semitic, especially the "c" ones (cumin, cinnamon, caraway). perhaps this is relevant because "q" and "k" both got borrowed as "k" in greek -> latin "c"
- english c happens to be used to spell both /c/ and /ch/ phonemes,
- words that started with kappa in greek -> latin "c", (caper, cardamom, coriander, etc etc)
- words pronounced "s" spelled "c" through french (celery).
- greek kh -> english c (chervil)
Might be worth a fun post about interesting travels of spice names.
It might well.
[Since a "spice rack" generally contains herbs as well as spices, and since Dan Jurafsky included some herbs (e.g. chervil) as well as spices in his note, maybe I should have worked with the original 40-item list, with 11 c-initial names. But now you've got the R scripts, so you can do it for yourself.]
[Update -- Guy Srinivasan writes:
Any lesson in statistics should include the odds of getting 7+ out of 22 randomly chosen words that start with the same letter, since you would have been just as surprised if 7+ 'B' words came up. Yes?
Well, actually, I would have been more surprised, since 'b' is quite a bit less frequent as an initial letter than 'c' is. But, OK, it's true that we're at risk of the kind of false positive that Carlo Emilio Bonferroni warned us about. Luckily, though, the Monte Carlo approach adapts very easily to this more complex situation:here's another Monte Carlo simulation in R that looks at the maximum number of same-letter nouns in 10,000 sets of 22, chosen at random from the 26,003 nouns in the CELEX2. About 2.6% of the time, 7 or more of the 22 words begin with the same letter. This corresponds to about 1 in 39 trials, which (for obvious reasons) is more often than the 1 in 200 trials where we'd expect 7 or more c-initial words -- but still less often than the 1 in 20 trials corresponding to the usual p < .05 criterion for statistical significance. Here are some relevant plots:
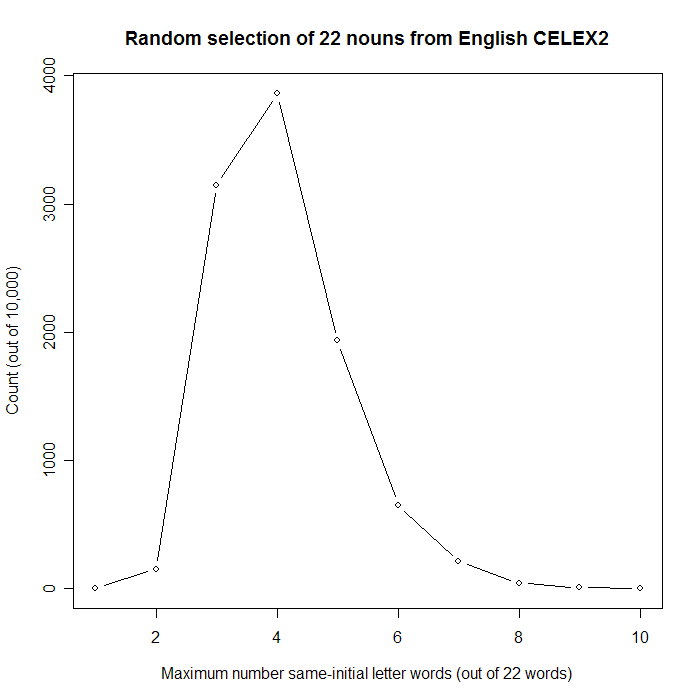
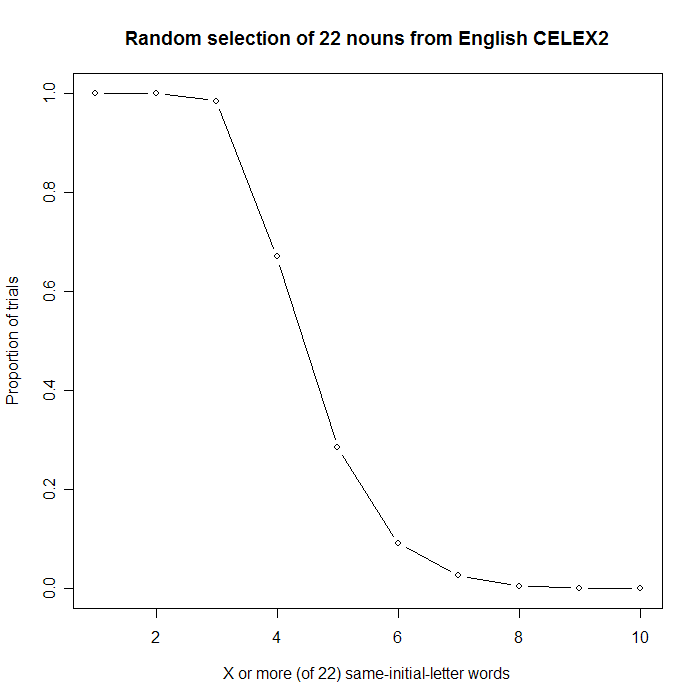
For the few übernerds who are still reading this, here is the list of CELEX2 noun initial-letter frequencies that I used, sorted in order of decreasing frequency. Each line has the letter, the count of nouns starting with that letter, and the proportion (out of 26,003):
s 3322 0.127754 c 2713 0.104334 p 2398 0.0922201 b 1619 0.062262 t 1495 0.0574934 m 1466 0.0563781 d 1425 0.0548014 a 1323 0.0508787 r 1262 0.0485329 f 1195 0.0459562 h 973 0.0374188 l 949 0.0364958 g 901 0.0346498 e 834 0.0320732 i 833 0.0320348 w 783 0.0301119 n 561 0.0215744 o 546 0.0209976 v 402 0.0154598 j 267 0.010268 k 232 0.00892205 u 225 0.00865285 q 140 0.00538399 y 81 0.00311503 z 52 0.00199977 x 6 0.000230743
]
[Update -- Rosie Redfield writes:
The high frequency of spice names beginning with C may just reflect the larger phenomenon of food words beginning with C.
If you check the index of a big practical cookbook (Fanny Farmer, Joy of Cooking), you'll find that a surprisingly large fraction of it is words beginning with C.
My preferred diet consists mainly of foods whose names begin with C: cake, candy, chocolate, coffee, cream, cookies, crackers, cheese , custard, casseroles...
Not to speak of cheese, creme caramel, couscous, calzone, and coconut cream pie. And chicken.]
[And Jason Wright wants to take it another step:
I don't think you've avoided the statistical fallacy mentioned by Guy Srinivasan.
So the chances of 7+ out of 22 random nouns starting with the same letter is 1/39. This doesn't mean something interesting is going on with spice names, though. Surely you would have also been surprised if 7 out of the 22 largest cities in your state started with "W"? Or if 7 out of the 22 unique brand names in your cupboard started with "K"? How many other sets of 22 nouns are in your kitchen? Your home? Your office? As soon as you count 20 such sets you might regularly encounter, the spices don't seem so unusual.
The problem with noticing something that seems unusual is that we so rarely notice the usual, so quantifying the unusual-ness is difficult.
Well, as Jason indicates, this line of reasoning suggests that no inductive generalization could ever be interesting, since there are indefinitely many features whose distribution can be examined relative to indefinitely many conditioning factors. Nevertheless, we do sometimes conclude that salient patterns are meaningful, and sometimes we turn out to be right about this, in the sense that we find a causal explanation for the pattern. Is the tendency of spice names to start with C one of the genuinely meaningful patterns, or is it one of the many accidental clusters of facts that lead to superstitions and the like? Beats me.
I guess you could ask a broader linguistic question: is there a general tendency for semantic classes of words to share initial sounds (and/or letters) more often than chance would predict? Phonetic symbolism is one reason that this might happen, and common cultural history might be another, but maybe there's an overall tendency towards quasi-regularization of this kind, simply because of rich-get-richer selective pressures in the psychodynamics of vocabulary development. I bet that some psycholinguists have looked into this. But this joke has gotten much deeper into the c-initial spice-name problem than I planned to go, so I'll ask a different question: why you hatin on C, man?]
[Update -- under the subject line "Spicing it up (for R aficionados only)", Ed Carney sent this:
Mulling your code, it occurred to me that you could model the samples using multinomial sampling (with "rmultinom()" in R). Each selection of 22 nouns could go into 26 different bins with probabilities associated with the CELEX2 lexicon. This method gives you the potential to construct the simulation for all of the letters at once, should such be your desire.
The relevant line "simul = rmultinom(Num,22,CELEX2)" performs 100,000 multinomial samples of 22 things in 26 bins using the probabilities calculated from the CELEX2 lexicon. This is returned as a two-dimensional matrix with 26 rows and 100,000 columns. Each row corresponding to a letter in the list you provided ('s', 'c', etc.). So, row 2 corresponds to letter 'c'. (This has the additional virtue of running a bit faster than the high-level "for" loop. It probably has an upper limit because of memory constraints, but I've run it as high as half a million samples on a laptop with 2Gbytes of RAM.)
Edward's script is here. This is the same thing that my second script does -- though rather than use the rmultinom() function, I did it the hard way, by running N trials, each of which chooses 22 numbers between 1 and 26,0003 and assigns the choice to one of the 26 letters of the alphabet, in proportion to the number of nouns in CELEX2 starting with that letter. Being impatient, I used only 10,000 trials, but re-running it with 100,000 took about 30 seconds on my laptop, whereas Edward's script only took 2 or 3 seconds. The result is the same, though.
Frankly, I did it the hard way because I didn't know about the rmultinom() function -- so I'll take that knowledge as my reward for going through the exercise.]
Posted by Mark Liberman at March 21, 2007 07:52 PM