March 01, 2008
Listening to Prozac, hearing effect sizes
As I've observed too often, it's hard for most people to talk or to think about differences in sampled distributions. Imagine, then, how hard it is to deal with models of sampled distributions of differences in sampled distributions. A recent case of this type seems to have reduced the American journalistic establishment to uncharacteristic silence.
The topic is a study by Irving Kirsch et al. that came out in PLoS Medicine on Monday, "Initial Severity and Antidepressant Benefits: A Meta-Analysis of Data Submitted to the Food and Drug Administration".
The British press gave this quite a bit of play: "Anti-depressants 'of little use'", BBC News; "Prozac, used by 40m people, does not work say scientists", The Guardian; "Antidepressant drugs don't work -- official study", The Independent; "Depression drugs don't work, finds data review", The Times; etc.
The relative lack of American coverage was noted by Kevin Drum at Washington Monthly ("Talking back to Prozac", 2/25/2008):
... what really drew my attention was the range of news outlets that reported this news. According to Google News, here they are: the Guardian, the Independent, the London Times, the Telegraph, the BBC, Sky News, the Evening Standard, the Herald, the Financial Times, and the Daily Mail. In fact, it's getting big play from most of these folks, including screaming front page treatment from some.
So what's the deal? Why is this huge news in Britain, where most of the stories are making great hay out of the amount of taxpayer money the NHS is squandering on these drugs, and completely ignored here in the U.S.?
There have since been a few American news reports. One was on Fox News, "Study: Antidepressants May Not Work in All Patients"; another was Steven Reinberg, "Only Severely Depressed Benefit From Antidepressants: Study", WaPo, 2/26/2008; and another was Laura Blue, "Antidepressants hardly help", Time Magazine, 2/26/2008. As far as I can tell, neither the NYT nor the AP have picked up the story at all.
Kevin seems to be on to something: the American media may not have "completely ignored" the study, in the end, but the American coverage has been not only smaller and later but also softer. The Fox headline was especially timid: "Antidepressants May Not Work in All Patients", and the lede was just as cautious:
Researchers from various U.S., U.K. and Canadian universities found that some patients taking antidepressants believe the drugs are working for them, but many times it is only a placebo effect.
The Fox story attributed its information to Sky News, a Murdoch TV outlet in the UK, rather than to the original study. But the Sky News coverage had a very different tone: "Depressed? Why The Pills Won't Help"; "Study Casts Doubt On Antidepressants" (lede: "Antidepressants are no more effective than dummy pills in most patients, researchers have found.")
And the coverage in the Times, also owned by Murdoch was even more baldly negative: "Depression drugs don't work".
I've waited a few days for the American coverage to catch up, without seeing much change. But this being Language Log, not Journalism Log, nor for that matter Psychiatry Log, what drew my professional attention to this case was the variable use of linguistic devices to present -- or misrepresent -- the original paper. Journalists are faced with the need to talk about the comparison of sampled distributions -- or worse, a model of sampled distributions of comparisons of sampled distributions -- while being unable to talk about models and distributions, instead being limited to generic propositions with a few standard quantifiers and modals.
Some writers got tangled up in sentences that mean very little, and certainly don't describe the results of the Kirsch et al. meta-analysis accurately:
some patients taking antidepressants believe the drugs are working for them, but many times it is only a placebo effect
not every antidepressant works for every patient
anti-depressants may not work in all patients
Other produced statements that are clear and contentful, but unfortunately are also false:
Four of the most commonly prescribed antidepressants, including Prozac, work no better than placebo sugar pills to help mild to moderate depression
They found that patients felt better but those on placebos improved as much as those on the drugs.
The new generation anti-depressants had no more effect than a dummy pill for people with mild or moderate depression.
Contrary to one's natural suspicion in such cases, the more baldly negative descriptions are not in this case more accurate. One of the most accurate presentations seems to me to be Laura Blue's story in Time Magazine ("Antidepressants hardly help", 2/26/2008):
There are really two issues at the heart of the controversy. One is the difference between "statistical significance" — a measure of whether the drug's effects are reliable, and that patient improvement is not just due to chance — and "clinical significance," whether those effects actually are big enough to make a difference in the life of a patient. The researchers behind this new paper did find that SSRI drugs have a statistically significant impact for most groups of patients: that is, there was some measurable impact on depression compared to the placebo effect. "But a very tiny effect may not have a meaningful difference in a person's life," says Irving Kirsch, lead author on the paper and a professor of psychology at the University of Hull in England. As it happens, only for the most severely depressed patients did that measurable difference meet a U.K. standard for clinical relevance — and that was mostly because the very depressed did not respond as much to placebos. The drug trials showed SSRI patients improved, on average, by 1.8 points on the Hamilton Depression Rating Scale, a common tool to rate symptoms such as low mood, insomnia, and lack of appetite. The U.K. authorities use a drug-placebo difference of three points to determine clinical significance.
The more troubling question concerns what kind of data is appropriate for analyzing a drug's efficacy. The companies are correct in claiming there is far more data available on SSRI drugs now than there was 10 or 20 years ago. But Kirsch maintains that the results he and colleagues reviewed make up "the only data set we have that is not biased." He points out that currently, researchers are not compelled to produce all results to an independent body once the drugs have been approved; but until they are, they must hand over all data. For that reason, while the PLoS Medicine paper data may not be perfect, it may still be among the best we've got.
Contrast Sarah Boseley, "Prozac, used by 40m people, does not work say scientists", The Guardian, 2./26/2008
Prozac, the bestselling antidepressant taken by 40 million people worldwide, does not work and nor do similar drugs in the same class, according to a major review released today.
The study examined all available data on the drugs, including results from clinical trials that the manufacturers chose not to publish at the time. The trials compared the effect on patients taking the drugs with those given a placebo or sugar pill.
When all the data was pulled together, it appeared that patients had improved - but those on placebo improved just as much as those on the drugs. [emphasis added]
Apparently in an attempt to make the point clear and strong, the Guardian's story crosses the line into plain falsehood, and so do the stories in several other major UK papers. Thus David Rose, "Depression drugs don't work, finds data review", Times, 2/26/2008:
The new generation anti-depressants had no more effect than a dummy pill for people with mild or moderate depression.
This case study in the public rhetoric of statistics is interesting and important enough to merit a closer look, so let's go back to the original article. Its authors used a Freedom of Information Act request to pry loose the results of "all clinical trials submitted to the US Food and Drug Administration (FDA) for the licensing of the four new-generation antidepressants for which full datasets were available" (fluoxetine, venlafaxine, nefazodone, and paroxetine). Significant parts of these datasets had not previously been published.
The final list comprised results from 35 studies, with the relevant numbers listed in their Table 1. Each row is a different study. Columns 3 and 4 are the average initial score on the "HRSD" (the Hamilton Rating Scale for Depression) and the average change in HRSD for patients in that study who got the drug; columns 8 and 9 are the average initial HRSD score and the average change in HRSD for the patients in that study who got the placebo ("sugar pill" or "dummy pill").
If we plot column 4 (average HRSD change in patients who got the drug) against column 9 (average HRSD change in patients who got the placebo), it's obvious to the eye that the drugs are having an effect different from the placebo. (Each red x is one clinical trial, with the average HRSD improvement in the drug group on the x axis, and the average HRSD improvement in the placebo group on the y axis.)
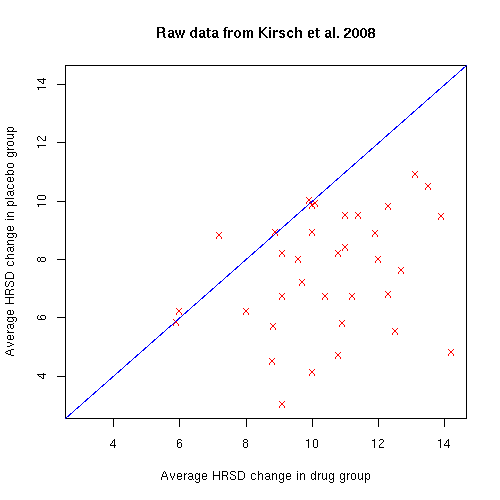
You can see that the placebo (or perhaps just the passage of time) is also having a positive effect on the HRSD values. But nearly all of the red x's are on the lower-right side of the blue line, indicating that in 32 out of 35 trials, the drug beat the placebo. This surely did not happen by chance. It's just not true that "those on placebo improved just as much as those on the drugs". In these studies, the drugs almost always had a greater positive effect than the placebo did.
The question is, how significant is the difference? And we're not talking about "statistical significance" -- we're interested in the "clinical significance" of the drug-minus-placebo effect. The definition of "clinical significance", which Kirsch et al. take from the UK's National Institute for Health and Clinical Excellence (NICE), depends not just on the average difference between drug and placebo groups, but also on the distributions of those effects. Specifically, the average measured outcomes are normalized by (i.e. divided by) the standard deviation of the measured outcomes.
(This is a common way to evaluate the "effect size" of a difference between two distributions -- there's a good explanation here, and an example here that may help to explain why this is a reasonable sort of thing to do.)
For example, in one of the Prozac studies (line 5 of Table 1), there were 297 people in the "drug" group, who began the study with an average HRSD score of 24.3, and ended with an average HRSD score of 15.48, for an average change of 8.82. There were 48 people in the "placebo" group, who began with an average HRSD of 24.3, and ended with an average of 18.61, for an average change of 5.69.
But these are the average results -- of course there was a great deal of individual variation. So it makes sense to divide the average change in HRSD score by the standard deviation of the change in HRSD score, producing what the authors call a "standardized mean difference".
If we do this in the cited case, then the effect size for the drug group is d=1.13, which is quite a large effect. But the effect size for the placebo group is d=0.72, which is also very respectable. And the difference in effect sizes between drug and placebo is d=0.41, which just misses the d=0.50 level that the British National Institute for Health and Clinical Excellence (NICE) has suggested should be the standard threshold for "clinical significance".
If we re-plot all the data using the d values rather than the change values, we get this:
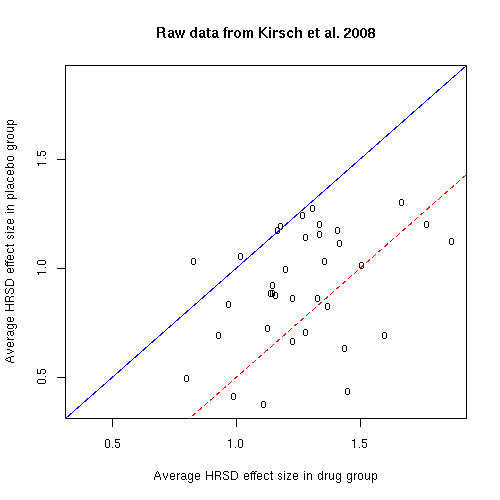
Of course, nearly all of the studies are still on the side of the blue line that indicates that the drug beat the placebo. However, only 10 of the 35 studies are on lower-right-hand side of the dashed red line, marking the NICE d=0.5 threshold for clinical significance.
Kirsch et al. go beyond this, to model the effect size as a function of the average initial HRSD score of patients in the study. I've reproduced their Figure 2, "Mean Standardized Improvement as a Function of Initial Severity and Treatment Group".
There are two points plotted for each trial: a red triangle for the "drug" group and a tan circle for the "placebo" group. The horizontal axis is the average initial HRSD score of the patients in the trial. The vertical axis is the improvement, measured in terms of effect size, i.e. "standardized mean difference (d), which divides change by the standard deviation of the change score SDC". The size of the plotted points represents their weight in the regression analysis (which I believe depends on the width of the error bars for the effect size estimates).
The solid red and dashed blue lines are curves fit to the data points, and the green region is the area where (according to the models) the "comparisons of drug versus placebo reach the NICE clinical significance criterion of d = 0.50".
But now we're talking about fitting a statistical model to the distribution across studies of effect sizes -- a measure of the difference between the distributions of outcomes in the "drug" and "placebo" groups -- as a function of initial severity. And there's no easy way to use the resources of ordinary non-statistician's English -- reference to groups, plurals, numbers and quantifiers like "most" and "some", negatives, modals like "may" -- to explain what's going on.
Where's Benjamin Lee Whorf when you need him? Seriously, linguistic anthropologists interested in language, thought and reality shouldn't be wasting their time with Eskimo words for snow. They should be investigating the way that different groups in our own culture describe differences in distributions.
[Update 3/15/2008 -- Peter Michael Gerdes writes:
I just wanted to point out that while the recent meta-analysis by Kirsch et. all about antidepressants only directly challenges the size of the effect it it embedded in a larger debate about whether these drugs are effective at all. As Kirsch and others have pointed out in prior papers a large fraction of patients and doctors are able to break the blind in these studies because the drugs have side effects the placebo lacks. In fact one study (which I can't remember the site for) suggested that the efficacy of the drugs was strongly correlated with the extent of side effects which at least shows that unblinding is a plausible explanation and other studies with older antidepressants have suggested that active placebos tend to be more effective than inactive ones.
I don't disagree with what you said in your post. If anything this is another point the media didn't cover very well. However, since you posted on the subject I thought you might want to know about this point. Anyway if you are interested I included some links to journal articles and comments by the involved scientists in my post on the subject, " Ghosts, UFOs, Yeti and Antidepressants?" (scroll down to the bottom for the references) .
Another relevant link is the editorial in Nature, " No More Scavenger Hunts", 3/6/2008. ]
Posted by Mark Liberman at March 1, 2008 07:54 AM