Language Log

Structures of words vs. structures of numbers

A paper has just been published in the Proceedings of the National Academy of Sciences (PNAS) that offers a new perspective on several recent themes. The authors are Rosemary A. Varley , Nicolai J. C. Klessinger , Charles A. J. Romanowski and Michael Siegal, and the paper is called "Agrammatic but numerate" (PNAS, March 1, 2005, vol. 102 no. 9, 3519-3524).

Here's the abstract:

A central question in cognitive neuroscience concerns the extent to which language enables other higher cognitive functions. In the case of mathematics, the resources of the language faculty, both lexical and syntactic, have been claimed to be important for exact calculation, and some functional brain imaging studies have shown that calculation is associated with activation of a network of left-hemisphere language regions, such as the angular gyrus and the banks of the intraparietal sulcus. We investigate the integrity of mathematical calculations in three men with large left-hemisphere perisylvian lesions. Despite severe grammatical impairment and some difficulty in processing phonological and orthographic number words, all basic computational procedures were intact across patients. All three patients solved mathematical problems involving recursiveness and structure-dependent operations (for example, in generating solutions to bracket equations). To our knowledge, these results demonstrate for the first time the remarkable independence of mathematical calculations from language grammar in the mature cognitive system. (The full paper is available on the PNAS site only to subscribers, but a copy of the .pdf version appears to be here.)

By "bracket equations" the authors mean arithmetic expressions in which the scope of operators is indicated by matched parentheses or brackets, e.g. 4 + 11 x (3 x 2) vs. (4 + 11) x 3 x 2.

The results are certainly striking. These patients are profoundly aphasic, as would be predicted given the extent of their dominant-hemisphere perisylvian lesions -- each row of images below belongs to one of the three patients surveyed:

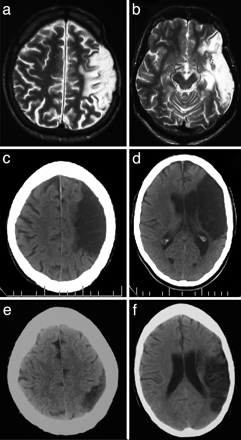
Their "severe disruptions in grammatical performance across language modalities" included ability to "[perform] no greater than at a chance level on understanding reversible sentences in both spoken and written modalities". ("Reversible sentences" are things like "The lady is calling the man", where it's equally plausible for the man to be calling the lady, so that you need to know more than the identity of the verb and the two noun phrases in order to guess correctly who did what to whom.) The patients also had other linguistic disabilities.

Despite their negligible syntactic ability in English, these patients could still do quite a bit of mathematics, of a kind that seems to require analogous syntactic processing. For example, in the "bracket expression" subtest,

Each patient calculated the sum of 90 expressions containing brackets. These included 64 expressions where the brackets were syntactic; i.e., if the participant adopted a serial order strategy, the result would be incorrect; e.g., 36 ÷ (3 x 2). The remaining interspersed 26 items were nonsyntactic: e.g., (3 x 3) - 6. The syntactic bracket expressions consisted of 38 items with a single level of embedded brackets and 26 items with apparent doubly embedded bracket structure. To avoid training performance, only 13 of these 26 items required serial computation of numbers contained within both sets of brackets, i.e., 50 - [(4 + 7) x 4] versus 3 x [(9 + 21) x 2]. Responses to the syntactic bracket expressions were scored for accuracy and presence of serial order calculation errors, e.g., 2 x [(5 x 2) + 5] = 25.

The results ( the three patients are called S.A., S.O. and P.R.):

	S.A.	S.O.	P.R.
Calculation accuracy	45/64	52/64	43/64
Serial order errors	4	1	2

This was just one of 14 mathematical subtests, and the patients' performance on all of them was strikingly better than their performance on analogous linguistic tasks.

This connects, at least loosely, to different sides of two recently-discussed stories. One is the role of language in mathematics, and especially in the most basic form of mathematical thought, namely counting. We discussed this in posts on the Pirahã (here, here, here) and the Mundurukú (here and here). The other is the role of recursion in language, discussed here, here, here and here.

In their conclusions, Varley et al. say that

In terms of the relationship between language and mathematics, our findings indicate considerable independence between the structure-dependent operations of language and number in an established cognitive architecture. Although agrammatic, all patients displayed sensitivity to, and use of, parallel syntactic principles in mathematics. Their responses are incompatible with a claim that mathematical expressions are translated into a language format to gain access to syntactic mechanisms specialized for language.

These results allow consideration of two alternative interpretations regarding the syntactic mechanisms of language and mathematics. One is that a common and domain-general syntactic mechanism underpins both language and mathematics but that mathematical expressions can gain direct access to this system without translation into a language format. In the case of patients with agrammatic aphasia, language representations are disconnected from the syntactic mechanism, but mathematical expressions can still gain access. The second alternative is that in the mature cognitive system, there are autonomous, domain-specific syntactic mechanisms for language and mathematics. Autonomy in the adult state does not entail independence throughout the developmental course of a system, and one mechanism might bootstrap the second. However, the presence of dissociations between mathematics and language in people with developmental language impairments indicates the potential for autonomous mechanisms throughout the lifespan and suggests that a language-specific mechanism does not bootstrap a nonlinguistic syntactic system.

[...]

With regard to the number lexicon, number words were unlikely to be the code in which calculations were performed; both S.A. and S.O. showed inefficiencies in using phonological and orthographic number words. Despite this, both were able to perform exact calculations involving two- and three-digit numbers. If, indeed, linguistic number words were the code in which calculations were performed, the inefficiencies inherent within these codes would have resulted in high error levels in mathematical tasks. All patients were efficient in processing Arabic numerals, suggesting that this code and its underlying conceptual base are sufficient for calculation.

The article left me with several questions.

One is whether this pattern (relative sparing of mathematical abilities) is typical of similarly agrammatic patients. If so, how has this fact remained unknown for so long? What other surprising dissociations are out there waiting to be discovered?

Another is how much use the patients made of pencil and paper techniques in solving the mathematical problems, since to some extent the learned procedures for arranging partial results on paper might substitute for (or at least assist) impaired ability to retain and manipulate the structure of mathematical expressions.

[Varley et al. link via email from Cosma Shalizi.]

 

Posted by Mark Liberman at March 2, 2005 12:12 AM