Language Log

Interpreting magical language

Yesterday I complained, again, about someone interpreting a slight statistical tendency in the complex behavior patterns of diverse groups (snap judgments of relative competence based on brief glimpses of politician's faces account for 5-10% of the variance in vote share) as a categorical fact about the behavior of all individuals at all times (election outcomes are entirely determined by the candidates' appearance). In response, Garrett Wollman writes:

I don't hold out much hope for the public coming to a better understanding of statistics and probability. It's been 223 years since the original text of this quotation was written:

The art of concluding from experience and observation consists in evaluating probabilities, in estimating if they are high or numerous enough to constitute proof. This type of calculation is more complicated and more difficult than one might think. It demands a great sagacity generally above the power of common people. The success of charlatans, sorcerors, and alchemists -- and all those who abuse public credulity -- is founded on errors in this type of calculation.

- Antoine Lavoisier and Benjamin Franklin, Rapport des commissaires chargés par le roi de l'examen du magnétisme animal (Imprimerie royale, 1784), trans. Stephen Jay Gould, "The Chain of Reason versus the Chain of Thumbs", Bully for Brontosaurus (W.W. Norton, 1991), p. 195

(This quotation is taken from <http://en.wikiquote.org/wiki/Antoine_Lavoisier>, but I'm the editor who put it there.)

In the context of Gould's article, he of course takes issue with the bit about "generally above the power of common people", but does not disagree with the sentiment in general. I'm feeling a bit too lazy to grab my copy of /Bully for Brontosaurus/ and reread that essay at the moment, but I suspect whatever Gould was deploring in 1991 can only have gotten worse over the ensuing sixteen years.

Well, one step at a time. I don't think it's unreasonable to expect that journalists and political commentators should come to understand things like how to interpret a scatter plot, what r² is and what it means, what it means to talk about two roughly normal distributions whose average values differ by about ten percent of a standard deviation, etc. More important -- and even easier -- they should learn to demystify general claims that come wrapped in the magical language of statistical sorcery, and ask simple questions like "how many of what?"

In fact, I suspect that things are getting better in most ways, not worse. There is a systematic effort in incorporate ideas about probability and statistics into school curricula in the U.S. -- here are some of the class projects assigned by a widely-used middle school mathematics text:

Is Anyone Typical? Students apply what they have learned in the unit to gather, organize, analyze, interpret, and display information about the "typical" middle school student.

The Carnival Game Students design carnival games and analyze the probabilities of winning and the expected values. They then write a report explaining why their games should be included in the school carnival.

Dealing Down Students apply what they have learned to a game. They then write a report explaining their strategies and their use of mathematics.

Estimating a Deer Population Students simulate a capture-recapture method for estimating deer populations, conduct some research, and write a report.

I don't know how well the nation's middle-school teachers understand these concepts -- probably there is a wide range of variation -- but perhaps those who don't know them will be learning along with their students.

My youngest son, who is in the sixth grade, has been given homework assignments based on the collection and interpretation of simple statistics about (for example) evaluations of a school trip, in which participant responses were divided into various subgroups (students vs. teachers, students in different grades, and so on. The techniques involved were fairly simple -- percentages and a few different sorts of graphs. But it asked them to calculate, represent and reason about group differences in (for example) the proportions of sixth graders vs. seventh graders who enjoyed the trip, at a level of sophistication that I would love to see regularly reproduced in the New York Times or the BBC News.

In my opinion, the biggest part of the problem is shock and awe in the face of unfamiliar ideas presented in an intimidating way. Seeing a new piece of jargon or an unfamiliar equation -- or even suspecting that they might see one if they looked further -- many people seem to freeze up and surrender their intellects, falling back on crude reasoning about group archetypes ("women are unhappy"), exaggerated and simplistic causal connections ("teachers' gesturing makes students learn 3 times better"), and naive reductionism ("the gene for X").

There are some cases where you need to understand an equation in order to evaluate a claim. For example, in order to evaluate the claims of Groseglose and Milyo in their widely-reported study "A Measure of Media Bias", you need to see that their mathematical model (apparently by mistake) embodies the assumption that conservatives care only about authoritativeness in deciding which sources to quote, whereas liberals weigh authoritativeness and ideology equally (see here and here for discussion). This is not very hard to understand. The right-hand side of the relevant equation is the sum of three terms, two of which are single variables while one is the product of two variables, of the form y = a + bx + e. You just have to reason a bit about what b and x are, and what it means to multiply them. This is not exactly the topos of presheaves on the poset of commutative subalgebras, you know?

But even that level of sophistication is not required, most of the time. Usually it's enough to say something like "wait a minute, never mind the beta coefficients and odds ratios for a minute, what are the numbers here? How many people diagnosed with the syndrome did you test, and how many of them had the genomic variation that you identified? And what were the same numbers for the control subjects? OK, so 77% of the people without the disease had this genomic variation, versus 84% of those with the disease? And what is the frequency of the diagnosis in the general population? About 2.7%? So if we used this as a screening test, assuming these proportions apply to the general population, let's see, the contingency table would look like this, right? And so, um, wait a minute, the false positive rate would be 97.1%? OK, thanks, now I see what's going on."

This is just middle-school math, plus a few simple but useful concepts like contingency table and false positive rate. And while there may be some intellectuals who are a little fuzzy on percentages, I think most educated Americans can (learn to) handle this stuff just fine. But when was the last time you saw this kind of discourse from a science journalist or a columnist?

I'm not trying to suggest that statistical analysis can or should be replaced by inspection of tables and graphs based on counts and simple derived quantities like proportions and percentiles. But we'd be a lot better off if (for example) journalists and other public intellectuals understood basic concepts built out of these simple parts -- histograms, contingency tables, and so on -- and insisted on understanding research at this basic level before getting to the more sophisticated methods.

The next step would be to understand and apply the general concept of "confidence interval". In fact, I think that most educated people have at least a blurry sort of idea about what this means, even if they don't apply the idea consistently

And beyond that, we might hope that someday a few percent of the population might understand factor analysis well enough to understand and evaluate the various debates about IQ.

And OK, sure, it would be nice if most the journalists assigned to the biomedical beat fully understood (say) how stratification is used to control for confounding variables in logistic regression, and why it can fail. But one step at a time.

[Update -- Rob Malouf sends in a link to post on Tritech.us from 7/13/2007, "Model Fitting, WSJ Style", which suggests that letting journalists loose with numbers and graphs might not always be the wisest policy:

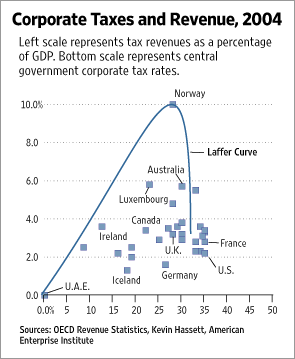
This is what happens when conservative journalists take a crack at statistics. An editorial in today's Wall Street Journal attempts to fit a relationship between a nation's corporate tax rate and the resulting tax revenue, as a fraction of gross domestic product (GDP). The amazing result is shown above, taken directly from the newspaper's website.

Now, few would argue that, taken over the entire unit interval, there should be some sort of unimodal relationship here -- clearly at both 0% and 100% taxation, there will be no tax revenue. This hypothesized relationship is known as the Laffer curve (I'll spare you the obvious pun). However, over the realized range of the data, there is a conspicuous increasing linear trend, albeit with much residual noise. This suggests that (1) this relationship is pretty messy, and not a very informative univariate model, and (2) the optimal rate may in fact lie beyond the upper range of the data! What is clear is that the article's author has no inkling of how to fit regression lines to data. Notice that if you extend the curve on the right hand side, it would intersect zero at about 32%. Apparently a complete tax revolt takes place (don't tell France and the US).

Now, I'm no Wall Street Journal basher (I'm a subscriber, in fact), but this is sophomoric journalism that only Fox News would be proud of. I expect better from one of the country's best national newspapers.

If I were the sort of person who sketched qualitative functional relationships on napkins, I might suggest that a plot of idiocy relative to education starts fairly high (at zero education), rises for a while with increasing education (because a little knowledge is a dangerous thing, especially in the case of arrogant people who think they know what the answer is before examining the facts), and eventually falls (because those of us who devote our lives to education need this faith). But I'm not, so I won't.]

Posted by Mark Liberman at October 27, 2007 10:14 AM