Language Log

Two slow takes from the canopy

To brighten your morning, here are a couple of lovely language-connected threads from Cosma Shalizi.

First, an amusing Q & A about nature and nurture, "...In Different Voices". Here's the key segment:

Q: How would you react to the idea that a psychological trait, one intimately linked to the higher mental functions, is highly heritable?

A: With suspicion and unease, naturally.

Q: It's strongly correlated with educational achievement, class and race.

A: Worse and worse.

Q: Basically nothing that happens after early adolescence makes an impact on it; before that it's also correlated with diet.

A: Do you work at the Heritage Foundation? Such things cannot be.

Q: What if I told you the trait was accent?

A: I'm sorry?

Q (in a transparently fake California accent): When you, like, say words differently than other people? who speak, like, the same language? because that's how you, you know, learned to say them from people around you?

A: Do you have a point to make, or are you just yanking my chain?

Q: Would you agree that accent has all the characteristics I just described?

A: Higher cognitive functions — heritable — class and race — not plastic after adolesence — correlation with diet, hah! — I guess I must.

Q: But would you say that there is any genetic or even congenital component to accent?

A: Not really. Obviously, some congenital conditions, like deafness or defects of the vocal chords, make it hard to impossible to acquire any accent. And I can imagine, though I don't know of anything, that there might be very specific mutations which make it hard to hear a distinction between a given pair of sounds, or easier to learn a specific distinction. But, in general, no, there is no non-trivial genetic component to accent.

Q: Then why were you worried that I was about to start channeling Arthur Jensen?

A: Because those are the sorts of claims usually trotted out by people who want to claim that something is innate, un-plastic, and usually invidiously distributed; sometimes there is a "sadly" to the claims of group inferiority, and sometimes, I think, that "sadly" is even genuine.

(This leaves out sex among the variables with which accent is strongly correlated; but perhaps that would have blurred the joke. People are happy to interpret statistical correlations as as essential properties of racial or ethnic groups, or of males vs. females -- and thus in modern terms, as evidence for genetic effects of race or sex. But when you put both factors together, those paleolithic natural-kinds intuitions get kind of confused. Then again, Cosma has already brought in diet, which opens another can of epidemiological worms.)

The Q & A continues in "Those Voices Again", which includes a typically Cosmic thought experiment:

Suppose that our new alien overlords showed up tomorrow, and after demonstrating that resistance is futile, decide to institute a selective breeding program. They tie everyone's tubes just before puberty, and then (say) age 25 everyone is given a test in which they must prove certain theorems about non-Abelian Yang-Mills field theories; those who pass are allowed to breed, those who fail are permanently sterilized. If this persisted for, say, a thousand years, I am quite confident that a randomly selected human being from 3007 will be much more likely to be able to do this than a randomly selected member of the present population.

Slightly more seriously (by which I mean only that it's slightly less funny, since both are highly serious), there's a suggestion about the nature and origins of the Flynn effect.

Next, there's a post "So You Think You Have a Power Law — Well Isn't That Special?", describing a recent paper by Clauset, Shalizi, and Newman, "Power-law distributions in empirical data", arxiv:0706.1062. This follows (and I would guess, results from) a series of weblog rants posts on the same topic. The paper's abstract:

Power-law distributions occur in many situations of scientific interest and have significant consequences for our understanding of natural and man-made phenomena. Unfortunately, the empirical detection and characterization of power laws is made difficult by the large fluctuations that occur in the tail of the distribution. In particular, standard methods such as least-squares fitting are known to produce systematically biased estimates of parameters for power-law distributions and should not be used in most circumstances. Here we describe statistical techniques for making accurate parameter estimates for power-law data, based on maximum likelihood methods and the Kolmogorov-Smirnov statistic. We also show how to tell whether the data follow a power-law distribution at all, defining quantitative measures that indicate when the power law is a reasonable fit to the data and when it is not. We demonstrate these methods by applying them to twenty-four real-world data sets from a range of different disciplines. Each of the data sets has been conjectured previously to follow a power-law distribution. In some cases we find these conjectures to be consistent with the data while in others the power law is ruled out.

The first author, Aaron Clauset, previously posted about this paper under the title "Power laws and all that jazz", with a different abstract:

Three Power Laws for the Physicists, mathematics in thrall,
Four for the biologists, species and all,
Eighteen behavioral, our will carved in stone,
One for the Dark Lord on his dark throne.

In the Land of Science where Power Laws lie,
One Paper to rule them all, One Paper to find them,
One Paper to bring them all and in their moments bind them,
In the Land of Science, where Power Laws lie.

Here's a fun sample figure from the paper:

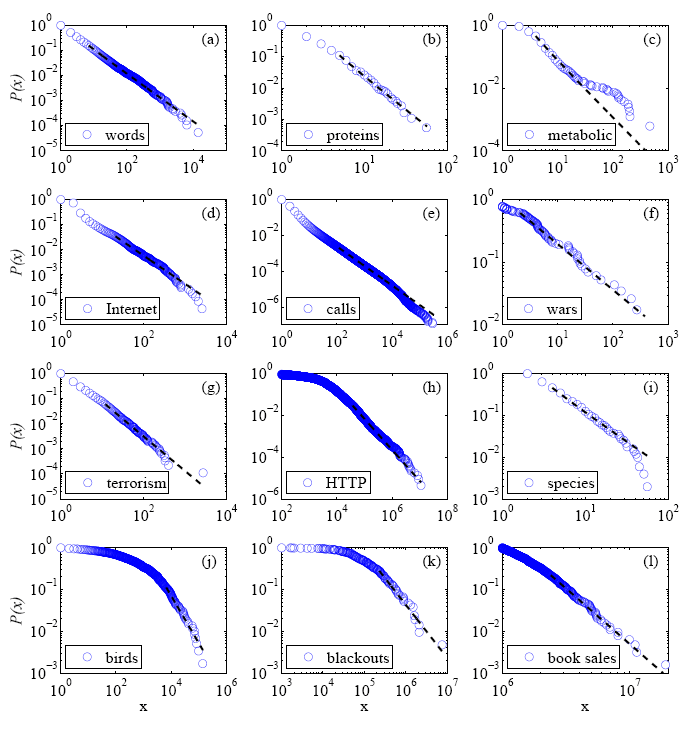
FIG. 8 The cumulative distribution functions P(x) and their maximum likelihood power-law fits, for the first twelve of our twenty-four empirical data sets. (a) The frequency of occurrence of unique words in the novel Moby Dick by Herman Melville. (b) The degree distribution of proteins in the protein interaction network of the yeast S. cerevisiae. (c) The degree distribution of metabolites in the metabolic network of the bacterium E. coli. (d) The degree distribution of autonomous systems (groups of computers under single administrative control) on the Internet. (e) The number of calls received by US customers of the long-distance telephone carrier AT&T. (f) The intensity of wars from 1816–1980 measured as the number of battle deaths per 10 000 of the combined populations of the warring nations. (g) The severity of terrorist attacks worldwide from February 1968 to June 2006 measured as the number of deaths greater than zero. (h) The size in bytes of HTTP connections at a large research laboratory. (i) The number of species per genus in the class Mammalia during the late Quaternary period. (j) The frequency of sightings of bird species in the United States. (k) The number of customers affected by electrical blackouts in the United States. (l) Sales volume of bestselling books in the United States.

The bottom line:

For most of the data sets considered the power-law model is in fact a plausible one, meaning that the p-value for the best fit is large. Other distributions may be a better fit, but the power law is not ruled out, especially if it is backed by additional physical insights that indicate it to be the correct distribution. In just one case—the distribution of the frequencies of occurrence of words in English text—the power law appears to be truly convincing in the sense that it is an excellent fit to the data and none of the alternatives carries any weight.

For seven of the data sets, on the other hand, the p-value is sufficiently small that the power-law model can be firmly ruled out. In particular, the distributions for the HTTP connections, earthquakes, web links, fires, wealth, web hits, and the metabolic network cannot plausibly be considered to follow a power law; the probability of getting a fit as poor as that observed purely by chance is very small in each case and one would have to be unreasonably optimistic to see power-law behavior in any of these data sets. (For two data sets—the HTTP connections and wealth distribution—the power law, while not a good fit, is nonetheless better than the alternatives, implying that these data sets are not well-characterized by any of the functional forms considered here.)

[...]

Note however that the log-normal is not ruled out for any of our data sets, save the HTTP connections. In every case it is a plausible alternative and in a few it is strongly favored. In fact, we find that it is in general extremely difficult to tell the difference between a log-normal and true power-law behavior. Indeed over realistic ranges of x the two distributions are very closely equal, so it appears unlikely that any test would be able to tell them apart unless we have an extremely large data set.

And there's code (in Matlab and R)! From Cosma's weblog post again:

Because this is, of course, what everyone ought to do with a computational paper, we've put our code online, so you can check our calculations, or use these methods on your own data, without having to implement them from scratch. I trust that I will no longer have to referee papers where people use GnuPlot to draw lines on log-log graphs, as though that meant something, and that in five to ten years even science journalists and editors of Wired will begin to get the message.

I'm less hopeful than Cosma about that last clause -- I mean, this sort of thing involves innumeracy way below the level of recognizing that frequency distributions exist, much less distinguishing among their functional forms. But hope is good.

Posted by Mark Liberman at June 25, 2007 06:01 AM